Cho hàm số: y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
a) Xác định m để hàm số đơn điệu trên R. Khi đó, hàm số đồng biến hay nghịch biến? Tại sao?
b) Với giá trị nào của m thì hàm số đạt cực đại tại x = 1 ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+)
m
2
+ 5m = 0 ⇔ 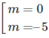
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
∆ ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.

a, Vì \(-6< 0\)nên hàm số (1) là hàm nghịch biến
Vì \(A\left(-1;6\right)\in\left(1\right)\)
\(\Rightarrow6=\left(-6\right).\left(-1\right)+m-1\)
\(\Leftrightarrow6=6+m-1\)
\(\Leftrightarrow m=1\)
b, Đths (1) cắt đths 2 tại 1 điểm trên trục tung nên
\(\hept{\begin{cases}m-1\ne3m-11\\x=0\\-6x+m-1=\left(m-1\right)x+3m-11\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m-1\ne3m-11\\m-1=3m-11\end{cases}}\)ko tìm đc m

a) Để hàm số đồng biến thì k(k-3)>0
\(\Leftrightarrow\left[{}\begin{matrix}k>3\\k< 0\end{matrix}\right.\)
b) Để hàm số nghịch biến thì k(k-3)<0
hay 0<x<3

\(\left(d\right):y=2\left(m-1\right)+3\)
\(A\in\left(d\right)\Rightarrow3=2\left(m-1\right).\left(-1\right)+3\)
\(\Leftrightarrow m=1\)
Tại \(m=1\Rightarrow\left(d\right):y=3\) .Khi đó hàm số ko đồng biến cũng không nghich biến

a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)

Bài 1:
a: Để hàm số đồng biến khi x>0 thì m-1>0
hay m>1
b: Để hàm số nghịch biến khi x>0 thì 3-m<0
=>m>3
c: Để hàm số nghịch biến khi x>0 thì m(m-1)<0
hay 0<m<1
a, đồng biến khi m - 1 > 0 <=> m > 1
b, nghịch biến khi 3 - m < 0 <=> m > 3
c, nghịch biến khi m^2 - m < 0 <=> m(m-1) < 0
Ta có m - 1 < m
\(\left\{{}\begin{matrix}m-1< 0\\m>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 1\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)

Đáp án A
Phương pháp:
Xét tính đúng sai của các đáp án dựa vào các kiến thức hàm số đồng biến, nghịch biến trên khoảng xác định.
Cách giải:
*2 sai vì với c 1 < c 2 bất kỳ nằm trong a ; b ta chưa thể so sánh được f c 1 và f c 2
*3 sai. Vì y' bằng 0 tại điểm đó thì chưa chắc đã đổi dấu qua điểm đó. VD hàm số y = x 3
*4 sai: Vì thiếu điều kiện tại f ' x = 0 hữu hạn điểm.VD hàm số y = 1999 có y ' = 0 ≥ 0 nhưng là hàm hằng.
Chú ý khi giải:
HS thường nhầm lẫn:
- Khẳng định số 4 vì không chú ý đến điều kiện bằng 0 tại hữu hạn điểm.
- Khẳng định số 3 vì không chú ý đến điều kiện đổi dấu qua nghiệm.
a) y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+) m2 + 5m = 0 ⇔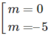
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
Δ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
b) Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
y′(1) = –3 m 2 – 3m + 6 = 0 ⇔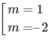
Mặt khác, y” = –6( m 2 + 5m)x + 12m
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0 , hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.