Tìm số nghịch đảo của 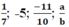 (a, b ∈ Z, a ≠ 0, b ≠ 0)
(a, b ∈ Z, a ≠ 0, b ≠ 0)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phân số nghịch đảo của phân số a b là b a a , b ∈ Z , a ≠ 0 , b ≠ 0

Câu 1:
Số đối của a/b là -a/b
\(\dfrac{a}{b}-\dfrac{c}{d}=\dfrac{ad-bc}{bd}\)
\(\dfrac{a}{b}\cdot\dfrac{c}{d}=\dfrac{ac}{bd}\)
Câu 2:
Số nghịch đảo của a/b là b/a
\(\dfrac{a}{b}:\dfrac{c}{d}=\dfrac{a}{b}\cdot\dfrac{d}{c}=\dfrac{ad}{bc}\)

a) Số nghịch đảo của \(\frac{a}{b}\) là \(\frac{b}{a}\)
b) \(-\frac{17}{7}.x=\frac{7}{-17}\Leftrightarrow x=\frac{7}{-17}:-\frac{17}{7}=\frac{49}{289}\)

Với a âm thì :
\(\dfrac{1}{a}\) cũng sẽ luôn luôn âm
Với a dương thì:
\(\dfrac{1}{a}\) cũng sẽ luôn luôn dương
Điều này xảy ra vì 1 là số dương,nếu mẫu là âm thì kq âm,và ngược lại

Số đối của phân số \(\dfrac{a}{b}\) là \(\dfrac{-a}{b}\) hoặc \(\dfrac{a}{-b}\) hoặc \(-\dfrac{a}{b}\)
Số nghịch đảo của phân số \(\dfrac{a}{b}\) là \(\dfrac{b}{a}\)
Số đối của \(\dfrac{a}{b}\) là \(\dfrac{-a}{b}\) hoặc \(\dfrac{a}{-b}\) hoặc \(-\dfrac{a}{b}\).
Số nghịch đảo của \(\dfrac{a}{b}\) là \(\dfrac{b}{a}\) hoặc \(\dfrac{-b}{-a}\).

Giúp với bà con ơi. Khó quá trời lun !!!!!!!!!!!!!!!!!!!!!!!!!
goi 3 do can tim la a , b ,c ( a,b,c la so tu nhien )
the de bai ta co : 1/a +1/b+1/c la so tu nhien
vi 1/a , 1/b ,1/c <=1 vay 1/a +1/b+1/c <=3
xet cac th :
th1 : 1/a +1/b+1/c =3 => a=b=xc=1 la nghiem
th2: 1/a +1/b+1/c=2 => a*b+b*c+a*c=2*a*b*c ( 1 )
gia su a = min (a,b,c ) => b*c= max ( a*b ,b*c ,a*c )
neu a=> 2 vay 2*a*b*c => 4*b*c > a*b+b*c+a*c vay a=1 hoac 2
+) voi a=1 ( 1 ) <=> 1+1/b+1/c =2
=> 1/b+1/c = 1 => b+c =b*c => b=c = 2
+) voi a=1 (1) 1/2+1/b+1/c =2
=> 1/b+1/c = 3/2 => b=1 x=2 hoac b=2 c=1
th3: 1/a +1/b+1/c=1 => a*b+b*c+a*c=a*b*c ( 2 )
gia su a = min (a,b,c ) => b*c= max ( a*b ,b*c ,a*c )
neu a=> 4 vay a*b*c => 4*b*c > a*b+b*c+a*c vay a=1,2 hoac 3
- Số nghịch đảo của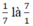
- Số nghịch đảo của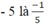
- Số nghịch đảo của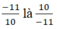
- Số nghịch đảo của