Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.
MH và MK
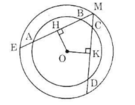
Hình 70
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK

a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK
a) Xét trong đường tròn nhỏ:
Theo định lí : trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.
Theo giả thiết suy ra gần tâm hơn, tức là .
b) Xét trong đường tròn lớn:
Theo định lí : trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.
Theo câu , ta có: .
c) Xét trong đường tròn lớn:
Vì (Định lý 2 - trang 103).
Vì (Định lý 2 - trang 103).
Theo câu , ta có:

a) Xét đường tròn nhỏ ta được .
b) Xét đường tròn lớn ta được .
c) Từ kết quả câu b) suy ra .

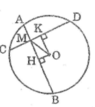
Ta có: HA = HB (gt)
Suy ra : OH ⊥ AB (đường kính dây cung)
Lại có : KC = KD (gt)
Suy ra : OK ⊥ CD (đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH (dây lớn hơn gần tâm hơn)
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
O M 2 = O H 2 + H M 2
Suy ra : H M 2 = O M 2 - O H 2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
O M 2 = O K 2 + K M 2
Suy ra: K M 2 = O M 2 - O K 2 (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: H M 2 > K M 2 hay HM > KM
Trong đường tròn lớn:
ME > MF => MH > MK