Giúp em 2 câu này với 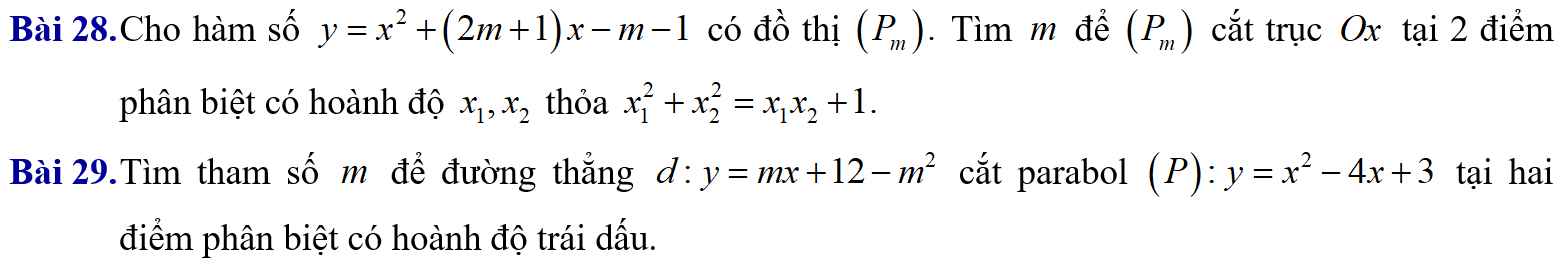
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Tọa độ điểm G là:
\(\left\{{}\begin{matrix}x_G=\dfrac{1+4+\left(-2\right)}{3}=\dfrac{3}{3}=1\\y_G=\dfrac{6-3+3}{3}=2\end{matrix}\right.\)

1: Tọa độ điểm G là:
\(\left\{{}\begin{matrix}x_G=\dfrac{1+4+\left(-2\right)}{3}=1\\y_G=\dfrac{6-3+3}{3}=2\end{matrix}\right.\)

ĐKXĐ: \(x\le4\)
\(\Leftrightarrow\left(x^3+3x^2+3x+1\right)+6\left(x+1\right)-\left(4-x\right)\sqrt{4-x}-6\sqrt{4-x}=0\)
\(\Leftrightarrow\left(x+1\right)^3+6\left(x+1\right)-\left(\sqrt{4-x}\right)^3-6\sqrt{4-x}=0\)
Đặt \(\left\{{}\begin{matrix}x+1=a\\\sqrt{4-x}=b\ge0\end{matrix}\right.\)
\(\Rightarrow a^3+6a-b^3-6b=0\)
\(\Rightarrow\left(a-b\right)\left(a^2+ab+b^2\right)+6\left(a-b\right)=0\)
\(\Rightarrow\left(a-b\right)\left[\left(a+\dfrac{b}{2}\right)^2+\dfrac{3b^2}{4}+6\right]=0\)
\(\Rightarrow a=b\)
\(\Rightarrow\sqrt{4-x}=x+1\left(x\ge-1\right)\)
\(\Rightarrow4-x=x^2+2x+1\)
\(\Rightarrow x^2+3x-3=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{-3+\sqrt{21}}{2}\\x=\dfrac{-3-\sqrt{21}}{2}< -1\left(loại\right)\end{matrix}\right.\)

\(c,x\left(x-20\right)-x+20=0\\ \Leftrightarrow x^2-20x-x+20=0\\ \Leftrightarrow x^2-21x+20=0\\ \Leftrightarrow\left(x-20\right)\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=20\\x=1\end{matrix}\right.\)
\(b,x^2-4+\left(x+2\right)\left(x-3\right)=0\\ \Leftrightarrow x^2-4+x^2-x-6=0\\ \Leftrightarrow2x^2-x-10=0\\ \Leftrightarrow\left(2x-5\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-2\end{matrix}\right.\)
a: Ta có: \(x\left(x-20\right)-x+20=0\)
\(\Leftrightarrow\left(x-20\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=20\\x=1\end{matrix}\right.\)
b: Ta có: \(x^2-4+\left(x+2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{5}{2}\end{matrix}\right.\)



Trl :
2x + 5x + 7x = 22.7
14x = 4.7
14x = 28
x= 28 : 14
x = 2
Hok tốt


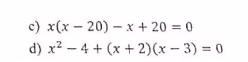 Mn giúp em 2 câu này với
Mn giúp em 2 câu này với



Bài 29:
PTHĐGĐ là:
\(x^2-4x+3=mx+12-m^2\)
\(\Leftrightarrow x^2-\left(m+4\right)x+m^2-9=0\)
Để (P) cắt (d) tại hai điểm phân biệt có hoành độ trái dấu thì \(m^2-9< 0\)
hay -3<m<3
Bài 28:
PT giao điểm của (Pm) và trục Ox là \(x^2+\left(2m+1\right)x-\left(m+1\right)=0\)
Để (Pm) cắt Ox tại 2 điểm pb thì \(\Delta=\left(2m+1\right)^2+4\left(m+1\right)=4m^2+8m+5>0\\ \Leftrightarrow4\left(m+1\right)^2+5>0\left(luôn.đúng\right)\)
Do đó (Pm) luôn cắt Ox tại 2 điểm pb
Theo định lí Vi-ét ta có \(\left\{{}\begin{matrix}x_1+x_2=-\left(2m+1\right)\\x_1\cdot x_2=-\left(m+1\right)\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1x_2+1\\ \Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=1\\ \Leftrightarrow\left(2m+1\right)^2+3\left(m+1\right)=1\\ \Leftrightarrow4m^2+7m+3=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-\dfrac{3}{4}\\m=-1\end{matrix}\right.\)