a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)

b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).

Ta có: R= OA = AA' = . = . = √3 (cm).

c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.

r = OA' = AA' = = (cm)

d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)

b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).

Ta có: R= OA = AA' = . = . = √3 (cm).

c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.

r = OA' = AA' = = (cm)

d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

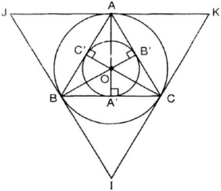
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước thẳng và compa).

+ Dựng đoạn thẳng AB = 3cm .

+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.

Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.

b) * Vẽ đường tròn:

Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực.

Dựng đường trung trực của đoạn thẳng BC và CA.

Hai đường trung trực cắt nhau tại O.

Vẽ đường tròn tâm O, bán kính OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.

* Tính bán kính đường tròn.

+ Gọi A’ là trung điểm BC ⇒ A’C = BC/2 = a/2.

và AA’ ⊥ BC

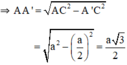
+ Do tam giác ABC là tam giác đều nên 3 đường trung trực đồng thời là ba đường trung tuyến

=> Giao điểm ba đường trung trực cũng là giao điểm ba đường trung tuyến

Suy ra O là trọng tâm tam giác ABC.

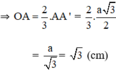
Vậy R = √3 (cm).

c) * Vẽ đường tròn:

Gọi A’; B’; C’ lần lượt là chân đường phân giác trong ứng với các góc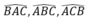 

Do tam giác ABC là tam giác đều nên A’; B’; C’ đồng thời là trung điểm BC; CA; AB.

Đường tròn (O; r) là đường tròn tâm O; bán kính OA’ = OB’ = OC’.

* Tính r:

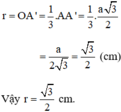
d) Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).

Sao OA=2/3 AA'

Hình như câu b chưa rõ lắm, tam giác ABC cân tại đâu?

đề chỉ ghi tam giác cân thôi bạn

\(h=\sqrt{b^2-\frac{a^2}{4}}\Rightarrow S=\frac{1}{2}ah=\frac{1}{2}a\sqrt{b^2-\frac{a^2}{4}}\)

\(R=\frac{abb}{4S}=\frac{ab^2}{\sqrt{4b^2-a^2}.a}=\frac{b^2}{\sqrt{4b^2-a^2}}\)

\(r=\frac{S}{p}=\frac{a\sqrt{b^2-\frac{a^2}{4}}}{a+2b}\)

tham khảo

https://cungthi.online/cau-hoi/cho-tam-giac-abc-tap-hop-nhung-diem-m-thoaman-4mambmc-30238-1652.html

Gọi G là trọng tâm của ΔABC

⇒ \(3\overrightarrow{MG}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\)

⇒ \(MA^2+MB^2+MC^{2^{ }}+2VT=9MG^2\)

⇒ VT = 9MG² - MA² + MB² + MC² 

⇒ \(\dfrac{a^2}{6}\) = 9MG² - MA² + MB² + MC²

MA² + MB² + MC² 

\(=\left(\overrightarrow{MG}+\overrightarrow{GA}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)^2\)

= 3MG² + 2\(\overrightarrow{MG}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)+ GA² + GB² + GC²

= 3MG² + \(GA^2+GB^{2^{ }}+GC^2\)

do \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)

Vậy ta có

\(\dfrac{a^2}{6}=6MG^2-GA^2-GB^2-GC^2\) 

⇔ \(\dfrac{a^2}{6}+\left(GA^2+GB^2+GC^2\right)=6MG^2\)(1)

Lưu ý, GA,GB,GC lần lượt bằng \(\dfrac{2}{3}\) độ dài các đường trung tuyến kẻ từ A,B,C. Nhưng do ΔABC đều nên chúng sẽ lần lượt bằng \(\dfrac{2}{3}\) đường cao kẻ từ A,B,C (đặt là h_a ; h_b; h_c)

Dễ dàng tìm được h_a = h_b = h_c = \(\dfrac{a\sqrt{3}}{2}\)

⇒ GA = GB = GC = \(\dfrac{a\sqrt{3}}{3}\)

⇒ GA² = GB² = GC² = \(\dfrac{a^2}{3}\)

⇒ GA² + GB² + GC² = a²

Thay vào (1)

\(\dfrac{a^2}{6}+a^2=3MG^2\) ⇔ MG² = \(\dfrac{7a^2}{18}\)

⇔ MG = \(\dfrac{a\sqrt{14}}{6}\)

Vậy R = \(\dfrac{a\sqrt{14}}{6}\)

Ai xem hộ sai chỗ nào vs

Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.

Ta có: BC = 2R

Giả sử đường tròn (O) tiếp với AB tại D, AC tại E và BC tại F

Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.

Suy ra: AD = AE = EO = OD = r

Theo tính chất hai tiếp tuyến cắt nhau ta có:

AD = AE

BD = BF

CE = CF

Ta có: 2R + 2r = BF + FC + AD + AE

= (BD + AD) + (AE + CE)

= AB + AC

Vậy AB = AC = 2(R + r)