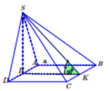
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a 2 , tam giác SAD cân tại S, mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích S.ABCD bằng 4 a 3 /3. Tính khoảng cách h từ B đến mặt phẳng (SCD).
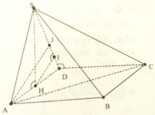
A. h = 2 3 a
B. h = 4 3 a
C. h = 8 3 a
D. h = 3 4 a



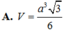
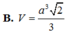
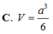
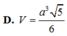


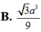
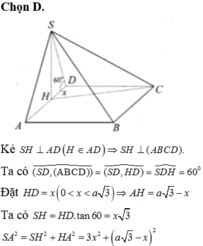


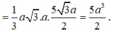

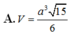
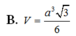
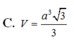
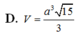

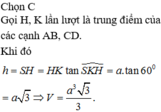
Đáp án B
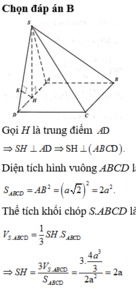
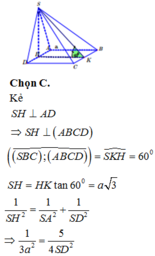
Gọi H là trung điểm của AD, vì ΔASD cân ở S nên SH ⊥ AD.
Vì (SAD)⊥(ABCD) nên SH ⊥ (ABCD). Kẻ HI ⊥ SD.
Vì DC ⊥ AD, DC ⊥ SH nên DC ⊥ (SAD). Do đó DC ⊥ HI.
Kết hợp với HI ⊥ SD, suy ra HI ⊥ (SDC).
Vì AB // (SDC) nên d(B; (SDC)) = d(A; (SDC)) = 2HI
Ta có
Ta lại có