Cho hình chóp S.ABCD có cạnh bên S A = ( 0 < α < 3 ) và các cạnh còn lại đều bằng 1. Tính theo a thể tích V của khối chóp S.ABCD.
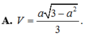
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
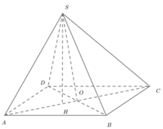
Phương pháp: Mấu chốt bài toán là chỉ ra được tam giác SAC vuông tại S.
Cách giải: Gọi O là giao điểm của AC và BD, H là hình chiếu của S lên mặt đáy.



Chọn A.
Phương pháp:
- Xác định góc giữa cạnh bên và mặt đáy.
- Tính diện tích đáy và chiều cao suy ra thể tích theo công thức
Chọn A.
Phương pháp:
- Xác định góc giữa cạnh bên và mặt đáy.
- Tính diện tích đáy và chiều cao suy ra thể tích theo công thức
V
=
1
3
S
h

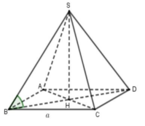

Chọn D
H là tâm đường tròn nội tiếp đáy.
Cách giải: Vì góc hợp bởi đường cao SH của hình chóp và các mặt bên của hình chóp đều bằng α nên H là tâm đường tròn nội tiếp ABCD.
Vì các cạnh bên hình chóp S.ABCD bằng a nên H là tâm đường tròn ngoại tiếp ABCD.
Vậy ABCD là hình vuông. Suy ra S.ABCD là hình chóp tứ giác đều.
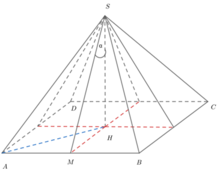
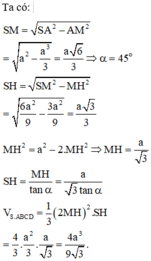

Chọn đáp án A
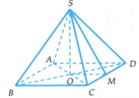
Gọi O là tâm của hình vuông ABCD, suy ra S O ⊥ A B C D
Gọi M là trung điểm của CD thì C D ⊥ O M mà C D ⊥ O M ⇒ C D ⊥ S O M
![]()
![]()
Đặt AB = 2x(x > 0) ⇒ O M = x
![]()
Do ∆ S O M vuông tại O nên S O = O M . tan S M O ⏜ = x . tan α
Do ∆ S O A vuông tại O nên S A 2 = S O 2 + O A 2
![]()
![]()
![]()
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 S O . S A B C D
Ta có
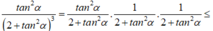
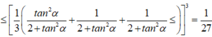
Suy ra 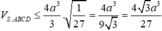
Dấu “=” xảy ra khi
![]()
![]()
Câu 2. Chọn B.