Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x 3 - x và đồ thị hàm số y = x - x 2
A. 9 4
B. 37 12
C. 81 12
D. 13
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 4 2018
+ Từ đồ thị của hàm số và a> 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:
Ta có : f’(x) = 4ax3+ 2bx
Đồ thị hàm số y= f’(x) đi qua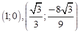 
ta tìm được a=1 và b= -2
Suy ra hàm số đã cho có dạng: f(x) =x4-2x2+d và f’(x) = 4x3-4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1
Vậy hàm số cần tìm là: y =x4-2x2+1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x4-2x2+1 =0 nên x=± 1
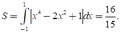
Chọn D.
NN
1
AH
Akai Haruma
Giáo viên
1 tháng 4 2021
Lời giải:
PT hoành độ giao điểm của 2 ĐTHS:
$x^2-4-(2x-4)=0\Leftrightarrow x^2-2x=0\Leftrightarrow x=0$ hoặc $x=2$
Diện tích hình phẳng giới hạn bởi 2 ĐTHS là:
\(\int ^2_0|x^2-4-(2x-4)|dx=\int ^2_0|x^2-2x|dx=\int ^2_0(2x-x^2)dx=\frac{4}{3}\)
CM
28 tháng 3 2018
Đáp án D
Phương trình hoành độ giao điểm của đồ thị f ( x ) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
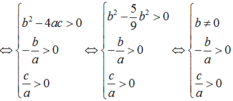
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a > 0 .
Khi đó
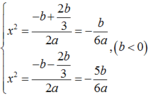
Suy ra x 1 = - - 5 b 6 a ; x 2 = - - b 6 a ; x 3 = - b 6 a ; x 4 = - b 6 a .
Do đồ thị hàm số f ( x ) nhận trục tung làm trục đối xứng nên ta có:
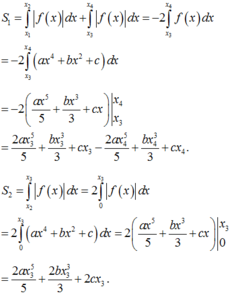
Suy ra
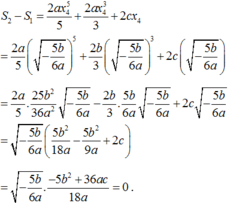
Vậy S 1 = S 2 hay S 1 S 2 = 1 .
Tìm hoành độ các giao điểm của hai đồ thị, ta có:
x 3 - x = x - x 3 <=> x 3 + x 2 - 2 x = 0
Vậy diện tích của hình phẳng tính là
Vậy chọn đáp án B.