Một hình nón có đỉnh S có bán kính đáý bằng 2 a 3 , góc ở đỉnh là 120 ∘ . Thiết diện qua đỉnh của hình nón là 1 tam giác. Diện tích lớn nhất S m a x của tam giác là bao nhiêu?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A

Xét thiết diện qua trục của hình nón N là ∆ A B C cân tại A.
Theo định lí hàm số sin ta có
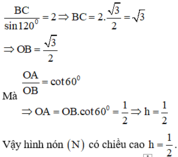

Đáp án D
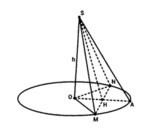
Thiết diện là tam giác SMN cân tại S.
Kẻ bán kính OA của hình nón
vuông góc với MN tại H



Chọn đáp án A.
Góc ở đỉnh hình nón là φ = 120 ° là góc tạo bởi khi mặt phẳng đi qua trục SO => O S C ^ = 60 °
Khi cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB nên mặt phẳng không chứa trục của hình nón.
Xét tam giác vuông SOC tại O:
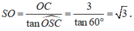
Xét tam giác vuông SOA tại O:
![]()
Do tam giác SAB đều:
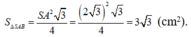
Đáp án đúng : A