Cho biểu thức f(x) = (x + 5)(3 - x). Tập hợp tất cả các giá trị của x thỏa mãn bất phương trình f(x) ≤ 0 là
A. x ∈ (- ∞ ;5) ∪ (3;+ ∞ )
B. x ∈ (3;+ ∞ )
C. x ∈ (-5;3)
D. x ∈ (- ∞ ;-5] ∪ [3;+ ∞ )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HK
1 tháng 5 2020
1/ \(f\left(x\right)\ge0\Leftrightarrow2x-4\ge0\Leftrightarrow x\ge2\)
2/ \(f\left(x\right)\le0\Leftrightarrow\left(x+5\right)\left(3-x\right)\le0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge-5\\x\ge3\end{matrix}\right.\\\left\{{}\begin{matrix}x\le-5\\x\le3\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge3\\x\le-5\end{matrix}\right.\)
6/ ĐKXĐ: \(x\ne2\)
\(f\left(x\right)=\frac{1}{3x-6}\le0\Leftrightarrow3x-6< 0\Leftrightarrow x< 2\)
H9
HT.Phong (9A5)
CTVHS
16 tháng 8 2023
Ta có bất phương trình thứ nhất:
\(2x+1< x+3\)
\(\Leftrightarrow2x-x< 3-1\)
\(\Leftrightarrow x\cdot\left(2-1\right)< 2\)
\(\Leftrightarrow x< 2\) (1)
Bất phương trình thứ hai:
\(5x\ge x-16\)
\(\Leftrightarrow5x-x\ge-16\)
\(\Leftrightarrow4x\ge-16\)
\(\Leftrightarrow x\ge-4\) (2)
Từ (1) và (2) ta có:
\(-4\le x< 2\)
15 tháng 8 2023
2x+1<x+3 và 5x>=x-16
=>2x-x<3-1 và 5x-x>=-16
=>x<2 và x>=-4
=>-4<=x<2
CM
31 tháng 5 2017
Chọn đáp án D
Số nghiệm của phương trình f ( x ) = m bằng
số giao điểm của đồ thị hàm số y = f ( x ) với
đường thẳng y = m
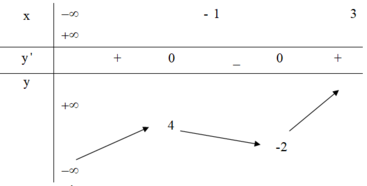
Từ bảng biến thiên suy ra phương trình có 3 nghiệm phân biệt khi − 2 < m < 4.
Chọn D.
Để f(x) ≤ 0 thì (x + 5)(3 - x) < 0
Vậy x ∈ (- ∞ ;-5] ∪ [3;+ ∞ ).