Cho hai đường thẳng xx' ,yy' cắt nhau tại O. Trên xx' lấy hai điểm A,B sao cho O là trung điểm AB. Trên yy' lấy C,D sao cho O là trung điểm CD ( A ∈ O x ; C ∈ O y )
So sánh AC và BD
A. AC = BD
B. AC < BD
C. AC > BD
D. AC ≥ BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
28 tháng 12 2018
Đúng(0)
Những câu hỏi liên quan
10 tháng 10 2020
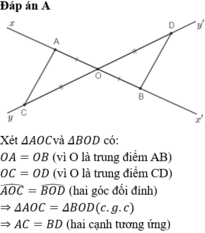
Vì AB và CD cắt nhau tại O là trung điểm mỗi đường nên ACBD là hình bình hành
=> AC//BD
20 tháng 4 2023
Xet ΔBML có
P,Q lần lươt là trung điểm của BM,BL
=>LP cắt MQ tại trọng tâm của ΔBML
Xét ΔBML có
BO là trung tuyến
BA=2/3BO
=>A la trọng tâm
=>LP cắt MQ tại A
9 tháng 8 2018
a, \(OA=AB=BC\left(gt\right)\Rightarrow CA=\frac{2}{3}CO\)
Tam giác MHC có: CO là đường trung tuyến và \(A\in CO,CA=\frac{2}{3}CO\left(cmt\right)\)
\(\Rightarrow A\) là trọng tâm của \(\Delta MHC\) nên đường trung tuyến HI đi qua điểm A.
b, BI là đường trung bình của \(\Delta AMC\left(gt\right)\Rightarrow BI//AM\)
AM là đường trung bình của \(\Delta OBN\left(gt\right)\Rightarrow AM//BN\)
Qua điểm B nằm ngoài đường thẳng AM, ta có: \(BI//AM,BN//AM\left(cmt\right)\) nên theo tiên đề Ơclít,
3 điểm B,N,I thẳng hàng.
Chúc bạn học tốt.