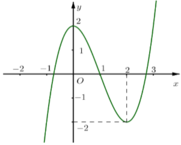
Cho hàm số f(x) = x3-3x2+ 2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đề phương trình
x
3
-
3
x
2
+
2
=
m
có nhiều nghiệm thực nhất A. m> -2 B. m> 0 C. -2< m< 2. D. m<...
Đọc tiếp
Cho hàm số f(x) = x3-3x2+ 2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đề phương trình x 3 - 3 x 2 + 2 = m có nhiều nghiệm thực nhất
A. m> -2
B. m> 0
C. -2< m< 2.
D. m< 2.
+ Ta có hàm số g(x) = x 3 - 3 x 2 + 2 = m là hàm số chẵn nên đồ thị nhận trục Oy làm trục đối xứng.
+ Khi x≥ 0 ; g(x) = x3- 3x2+ 2
Do đó; đồ thị hàm số g(x) = x 3 - 3 x 2 + 2 có dạng như hình vẽ.
+ Dựa vào đồ thị suy ra phương trình x 3 - 3 x 2 + 2 = m có nhiều nghiệm thực nhất khi và chỉ khi -2< m< 2.
Chọn C.