Cho 3 số dương có tổng là 65 lập thành một cấp số nhân tăng, nếu bớt một đơn vị ở số hạng thứ nhất và 19 đơn vị ở số hạng thứ ba ta được một cấp số cộng. Tìm số lớn nhất trong 3 số đó?
A. 5; 20; 40
B. 40
C. 45
D.5; 15; 45
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
17 tháng 9 2023
Gọi công bội của cấp số nhân là q => b=a.q; c=a.q^2
Gọi công sai của cấp số cộng là d => b=a+2d; c=a+8d
Ta có: a.q=a+2d => \(q=\dfrac{a+2d}{a}=1+2\dfrac{d}{a}\)
\(a.q^2=a+8d\Rightarrow q^2=\dfrac{a+8d}{a}=1+8\dfrac{d}{a}\)
Suy ra \(\left(1+2\dfrac{d}{a}\right)^2=1+8\dfrac{d}{a}\Rightarrow\dfrac{d}{a}=1\left(d\ne0\right)\)
=> b=a+2a=3a; c=a+8a=9a
Theo bài ra a+b+c=26 => a+3a+9a=13a=26 => a=2; b=6; c=18
Vậy ba số cần tìm là a=2; b=6; c=18
CM
25 tháng 5 2019
+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x
Theo giả thiết ta có hệ phương trình
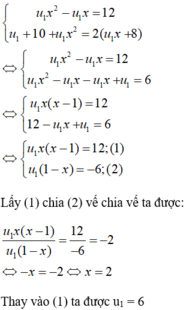
+ Tổng của năm số hạng đầu của CSN là:
CM
27 tháng 1 2019
Tổng hơn số hạng thứ nhất 73 .vậy số hạng thứ hai là 73 Số hạng thứ nhất là 73-28=45 Hai số Cần tìm 45. ;73 Hình tăng thêm là hình tam giác. hình tam giác và hình thang sẽ có chung đường cao. Tìm đường cao tam giác là 50.7 × 2 : 6.5 = 15.6. Diện tích hình thang là ( 30,5 + 24 ) × 15.6 : 2 = 425,1
9 tháng 7 2023
1:
Số thứ nhất bằng tổng hai số trừ đi số hạng thứ hai
=>Số thứ nhất là 78
4:
Gọi hai số cần tìm là a,b
Theo đề, ta có:
a+b-b=59 và b-a=38
=>a=59 và b=38+59=97
=>Tổng hai số là 59+97=156
Chọn C.
Gọi u1; u2; u3 theo thứ tự đó lập thành một cấp số nhân.
Theo đề: u1 – 1; u2; u3 – 19 theo thứ tự đó lập thành một cấp số cộng.
Ta có: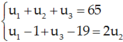
Lấy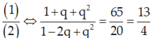
⇔ 4(1 + q + q2) = 13(1 – 2q + q2)
⇔ 9q2 – 30q + 9 = 0 ⇔ q = 3 ∨ q = 1/3
Vì u1; u2; u3 theo thứ tự lập thành cấp số nhân tăng dần nên chọn q = 3 khi đó u1 = 5
Do đó u1 = 5; u2 = 15; u3 = 45
Vậy số lớn nhất trong 3 số là 45.