nên không tồn tại cặp số u,v nào tồn tại thỏa mãn điều kiện trên.

a) S = 12, P = 28  ⇒   S 2   –   4 P   =   32   >   0

⇒ u, v là hai nghiệm của phương trình:  x 2   –   12 x   +   28   =   0 .

Có a = 1; b = -12; c = 28   ⇒   Δ ’   =   ( - 6 ) 2   –   28   =   8   >   0

Phương trình có hai nghiệm  x 1   =   6   +   2 √ 2 ;   x 2   =   6   -   2 √ 2

Vì u > v nên u = 6 + 2√2 và v = 6 - 2√2

b) S = 3; P = 6  ⇒   S 2   –   4 P   =   - 15   <   0

Vậy không tồn tại u, v thỏa mãn yêu cầu.

S = -8; P = -105 ⇒ S2 – 4P = (-8)2 – 4.(-105) = 484 > 0

⇒ u và v là hai nghiệm của phương trình: x2 + 8x – 105 = 0

Ta có: Δ’ = 42 – 1.(-105) = 121 > 0

Phương trình có hai nghiệm:

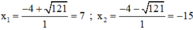
Vậy u = 7 ; v = -15 hoặc u = -15 ; v = 7.

a)   S   =   32 ;   P   =   231   ⇒   S 2   –   4 P   =   322   –   4 . 231   =   100   >   0

⇒ Tồn tại u và v là hai nghiệm của phương trình:  x 2   –   32 x   +   231   =   0 .

Ta có:  Δ   =   ( - 32 ) 2   –   4 . 231   =   100   >   0

⇒ PT có hai nghiệm:

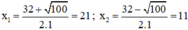
Vậy u = 21 ; v = 11 hoặc u = 11 ; v = 21.

b) S = -8; P = -105  ⇒   S 2   –   4 P   =   ( - 8 ) 2   –   4 . ( - 105 )   =   484   >   0

⇒ u và v là hai nghiệm của phương trình:  x 2   +   8 x   –   105   =   0

Ta có:  Δ ’   =   4 2   –   1 . ( - 105 )   =   121   >   0

Phương trình có hai nghiệm:

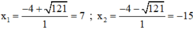
Vậy u = 7 ; v = -15 hoặc u = -15 ; v = 7.

c) S = 2 ; P = 9 ⇒  S 2   –   4 P   =   2 2   –   4 . 9   =   - 32   <   0

⇒ Không tồn tại u và v thỏa mãn.

H = 32; U = 231 => H^2 - 4U = 32^2 - 4.231 = 100 > 0

tồn tại u và v là 2 nghiệm pt: x^2 - 32x + 231 = 0

ta có: \(\Delta=\left(-32x\right)^2-4.231=100>0\)

pt có 2 nghiệm: 

\(x_1=\frac{32+100}{2.1}=21;x_2=\frac{32-\sqrt{100}}{2.1}=11\)

\(\Rightarrow\hept{\begin{cases}u=21;v=11\\u=11;v=21\end{cases}}\)

Hai số u và v với u +v =4 và uv =19 nên nó là nghiệm của phương trình  x 2  - 4x +19 = 0

∆ ’=  - 2 2  – 1.19= 4 - 19=-15 < 0

Phương trình vô nghiệm nên không có giá trị nào của u và v thỏa mãn điều kiện bài toán

S = 3; P = 6 ⇒ S2 – 4P = -15 < 0

Vậy không tồn tại u, v thỏa mãn yêu cầu.

S = 12, P = 28 ⇒ S2 – 4P = 32 > 0

⇒ u, v là hai nghiệm của phương trình: x2 – 12x + 28 = 0.

Có a = 1; b = -12; c = 28 ⇒ Δ’ = (-6)2 – 28 = 8 > 0

Phương trình có hai nghiệm x1 = 6 + 2√2; x2 = 6 - 2√2

Vì u > v nên u = 6 + 2√2 và v = 6 - 2√2