Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:
y = 3 - 2 x y = 3 x - 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 3 2019
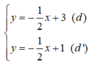
Xét (d):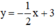 
có a = 
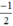; b = 3
(d’):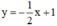 
có a’ = 
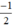; b’ = 1.
Có a = a’; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ phương trình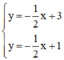 
vô nghiệm
CM
16 tháng 7 2017
Ta có:
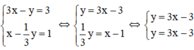
Ta có: a = a’=3; b = b’ = -3
Nhận thấy hai đường thẳng trên trùng nhau
⇒ Hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
CM
19 tháng 2 2019
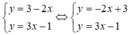
a) Xét (d): y = -2x + 3 có a = -2; b = 3
(d’) : y = 3x – 1 có a’ = 3 ; b’ = -1.
Có a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ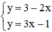 
có nghiệm duy nhất.
b)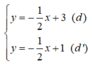 
Xét (d):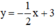 
có a = 
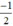; b = 3
(d’):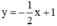 
có a’ = 
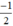; b’ = 1.
Có a = a’; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ phương trình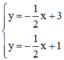 
vô nghiệm.
c) Ta có: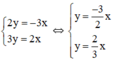 
Xét (d): y =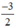 
x có a = 
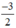; b = 0
(d’) : y =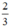 
x có a’ = 
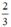; b’ = 0
Ta có: a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ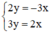 
có nghiệm duy nhất.
d) Ta có:
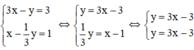
Ta có: a = a’=3; b = b’ = -3
Nhận thấy hai đường thẳng trên trùng nhau
⇒ Hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
+ Xét hệ (I):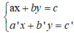 
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.
CM
25 tháng 3 2019
Ta có: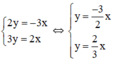 
Xét (d): y =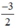 
x có a = 
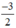; b = 0
(d’) : y =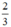 
x có a’ = 
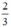; b’ = 0
Ta có: a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ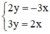 
có nghiệm duy nhất.
CM
13 tháng 4 2018
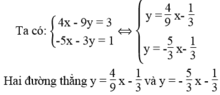
cắt nhau vì chúng có hệ số góc khác nhau.
Vậy hệ phương trình có một nghiệm duy nhất.
CM
26 tháng 7 2019
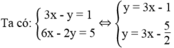
Vì hai đường thẳng có hệ số góc đều bằng 3 nhưng tung độ gốc khác nhau (-1 ≠ - 5/2 ) nên chúng song song với nhau.
Vậy hệ phương trình vô nghiệm.
CM
1 tháng 2 2019
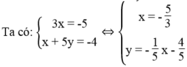
Vì đường thẳng x = - 5/3 song song với trục tung còn đường thẳng y = - 1 5 x - 4 5 cắt hai trục tọa độ nên chúng cắt nhau.Vậy hệ phương trình có một nghiệm duy nhất.
CM
5 tháng 12 2019
Vì đường thẳng y = 3 song song với trục hoành còn đường thẳng y = - 23 8 x + 25 4 cắt hai trục tọa độ nên chúng cắt nhau.
Vậy hệ phương trình có một nghiệm duy nhất.
CM
5 tháng 9 2019
x = 2 2 x - y = 3
Đường thẳng (d): x = 2 song song với trục tung.
Đường thẳng (d’): 2x – y = 3 không song song với trục tung
⇒ (d) cắt (d’)
⇒ Hệ có nghiệm duy nhất.
Vẽ (d): x = 2 là đường thẳng đi qua (2 ; 0) và song song với trục tung.
Vẽ (d’): 2x - y = 3
- Cho x = 0 ⇒ y = -3 được điểm (0; -3).
- Cho y = 0 ⇒ x = 1,5 được điểm (1,5 ; 0).
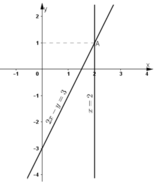
Ta thấy hai đường thẳng (d) và (d’) cắt nhau tại A(2; 1).
Vậy hệ phương trình có nghiệm (2; 1).
Xét (d): y = -2x + 3 có a = -2; b = 3
(d’) : y = 3x – 1 có a’ = 3 ; b’ = -1.
Có a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ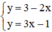
có nghiệm duy nhất.