Một bộ nguồn gồm 20 acquy giống nhau, mỗi acquy có suất điện động E 0 = 2 V và điện trở trong r 0 = 0,1 Ω , được mắc theo kiểu hỗn hợp đối xứng. Điện trở R = 2 Ω được mắc vào hai cực của bộ nguồn này. Để dòng điện chạy qua điện trở R có cường độ cực đại thì bộ nguồn này phải gồm bao nhiêu dãy song song, mỗi dãy gồm bao nhiêu acquy mắc nối tiếp ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay các trị số đã cho và tìm được vào (1) ta tìm được giá trị cực đại của I là : I m a x = 10 A

đáp án B
ξ b = m ξ = 2 m r b = m r n = 0 , 1 m n = m 2 120 ⇒ I = ξ b R + r b = 2 m R + m 2 120 = 240 m + 120 m ≤ 120 R
⇒ I max = 120 R ⇔ m = 120 R = 6 ⇒ n = 2

Chọn: B
Hướng dẫn:
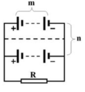
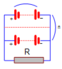
Cho bộ nguồn gồm 6 acquy giống nhau được mắc thành hai dãy song song với nhau, mỗi dãy gồm 3 acquy mắc nối tiếp với nhau. Mỗi acquy có suất điện động E = 2 (V) và điện trở trong r = 1 (Ω).
- Mỗi dãy gồm 3 acquy mắc nối tiếp với nhau nên suất điện động và điện trở trong của mỗi dãy là
![]()
- Hai dãy giống nhau mắc song song với nhau nên suất điện động và điện trở trong của bộ nguồn lần lượt là
![]()


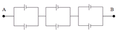

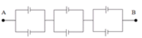

Giả sử bộ nguồn này có m dãy, mỗi dãy gồm n nguồn mắc nối tiếp, do đó nm = 20. Suất điện động và điện trở trong của bộ nguồn này là :
E b = n E 0 = 2n;
Áp dụng định luật Ôm cho toàn mạch ta tìm được cường độ dòng điện chạy qua điện trở R là :
Để I cực đại thì mẫu số của vể phải của (1) phải cực tiểu. Áp dụng bất đẳng thức Cô-si thì mẫu số này cực tiểu khi : mR = n 0 . Thay các giá trị bằng số ta được : n = 20 và m = 1.
Vậy để cho dòng điện chạy qua điện trở R cực đại thì bộ nguồn gồm m = 1 dãy với n = 20 nguồn đã cho mắc nối tiếp.