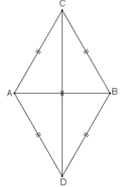
Xét ΔACD và ΔBCD, ta có:

AC = BC (= AB)

CD cạnh chung

AD = BD (= AB)

Suy ra: ΔACD = ΔBCD(c.c.c)

Bạn chỉ cần viết lại khúc từ cung tròn tâm A đến ở C và D rồi suy ra AC=AB=AD=BD=BC là đc nhé còn lại tự giải

a: xét tam giác abc và tam giác abd có 

- ab chung

- ac=ad

- cd=bd

suy ra tam gics abc= tam giác abd (c-c-c)

b:xét tam giác acd và tam giác bcd có

-cd chung

- ac=ad

- cb=bd

suy ra tam giác acd= tam giác bcd (c-c-c)

hơ

a: Xét ΔABC và ΔABD có

AB chung

BC=BD

AC=AD
Do đó: ΔABC=ΔABD

b: Xét ΔACD và ΔBCD có

AC=BC

CD chung

AD=BD

Do đó:ΔACD=ΔBCD

a)            Xét ΔABC và ΔABD , ta có :

                         AC = AD       

                         BC = BD

                    AB là cạnh chung
⇒ ΔABC = ΔABD

b)            Xét ΔACD và ΔBCD , ta có :

                         AC = BC

                         AD = BD

                    CD là cạnh chung

⇒ ΔACD = ΔBCD

                              CHÚC B HỌC TỐT NHA !!! 

Hướng dẫn:

Có: BM = BN ( = BA ) => B thuộc đường trung trực  của MN (1)

Có: AM= AN (= AB ) => A thuộc đường trung trực của MN (2)

Từ (1) , (2) => AB là đường trung trực MN => AB vuông góc MN.

Vì M, N thuộc (B; AB)

=>MB=NB(1)

Vì M, N thuộc (A; AB)

=>MA=MB(2)

Từ (1) và (2)

=>B, A nằm trên trung trực của MN(3)

=>AB vuông với MN(vì AB là tt MN có được từ điều 3)