Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d ( d ⊥ BC). Gọi H là chân đường cao hạ từ đỉnh A đến đường thẳng BC. Diện tích tam giác tỉ lệ thuận với chiều cao AH không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


S A B C là hàm số của chiều cao AH.
Gọi y là diện tích của
△
ABC (
c
m
2
) và x là độ dài AH (cm) thì 
Đồ thị như hình bên.
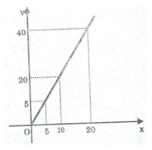

a:
| AH | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| S | 2 | 4 | 6 | 8 | 10 | 20 | 30 | 40 |
b: 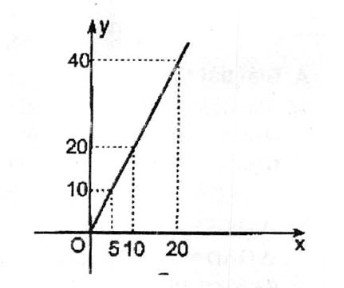
c: Diện tích tam giác tỉ lệ thuận với chiều cao

Điền vào ô trống
| Độ dài AH (cm) | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| S A B C ( c m 2 ) | 2 | 4 | 6 | 8 | 10 | 20 | 30 | 40 |

Gọi h (AH) là đường cao của \(\Delta ABC\) thì h là hằng số không đổi và cạnh đáy BC bằng a cố định .
Ta có : \(S_{ABC}=\dfrac{1}{2}BC.AH=\dfrac{1}{2}a.h\) không đổi .
Vậy diện tích tam giác ABC luôn không đồi nếu có đáy BC cố định và đỉnh A di động trên 1 đường thẳng d cố định song song với đường thẳng BC .

Đường thẳng d cố định song song với đường thẳng BC cố định nên khoảng cách hai đường thẳng d và BC là không đổi.
Tam giác ABC có cạnh đáy BC không đổi, chiều cao AH là khoảng cách giữa 2 đường thẳng song song không đổi.
Vậy điểm A thay đổi trên đường thẳng d // AB thì diện tích tam giác ABC không đổi.

Gọi h là đường cao của tam giác ABC thì h là hằng số không đổi và cạnh đấy BC = a cố định.
Ta có \(S_{ABC}=\frac{1}{2}.BC.AH=\frac{1}{2}ah\) không đổi.
Vậy có đpcm

Kẻ AK vuông góc BC. Gọi G là trọng tâm tam giác ABC và N là trung điểm BC. Kẻ GI vuông góc với AK
\(\Rightarrow\)GI // BC
\(\Rightarrow\frac{IK}{AK}=\frac{IK}{3}=\frac{GN}{AN}=\frac{1}{3}\)
\(\Rightarrow IK=1\)
Mà IK chính là khoản cách từ G đến BC
Vậy trọng tâm G nằm trên đường thẳng song song với BC và cách BC 1 khoản là 1 cm

a: Đặt AH=x
=>BC=4x
Theo đề, ta có: 1/2*4x*x=72
=>2x^2=72
=>x=6
b: Xét ΔCAB có MN//AB
nên ΔCMN đồng dạng với ΔCBA
=>S CMN/ SCBA=(CM/CB)^2=1/4
=>SCMN=18cm2
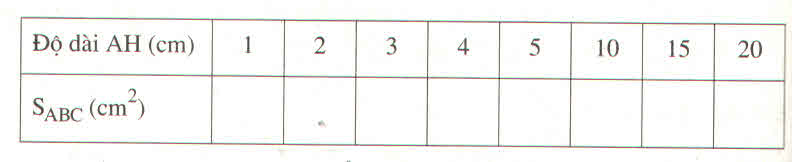

Diện tích của tam giác tỉ lệ thuận với chiều cao.