Hai đường chéo của hình chữ nhật chia hình chữ nhật thành bốn tam giác. Diện tích của các tam giác đó có bằng nhau không? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

TP
14 tháng 12 2017
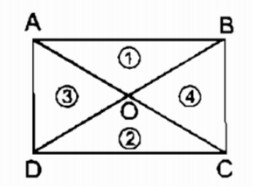
Gọi O là giao điểm hai đường chéo hình chữ nhật ABCD
⇒ OA = OB = OC = OD (tính chất hình chữ nhật)
∆ OAB = ∆ OCD (c.g.c) ⇒SOAB=SOCD⇒SOAB=SOCD (1)
∆ OAD = ∆ OBC (c.g.c) ⇒SOAD=SOBC⇒SOAD=SOBC (2)
Kẻ AH ⊥ BD
SOAD=\(\dfrac{1}{2}AH.OD\)
SOAB=\(\dfrac{1}{2}AH.OB\)
Suy ra: SOAD=SOAB (3)
Từ (1), (2) và (3) suy ra:
SOAB=SOBC=SOCD=SODA

CM
6 tháng 4 2018
Ta ghép như sau:
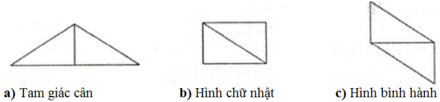
Diện tích 3 hình này đều bằng nhau vì cùng bằng tổng diện tích của hai tam giác vuông ban đầu.

21 tháng 4 2017
Cắt hai tam giác vuông bằng nhau từ một tấm bìa, chẳng hạn ta được hai hình sau:
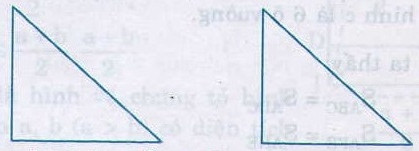
Ghép hai tam giác trên để tạo thành:
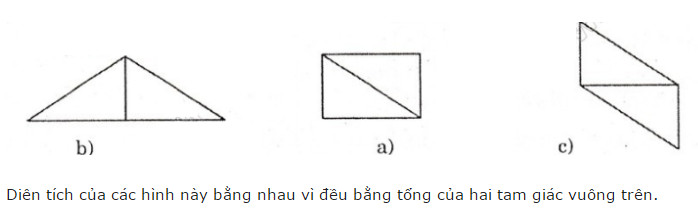


Gọi O là giao điểm 2 đường chéo hình chữ nhật ABCD.
Ta có: OA = OB = OC = OD (tính chất hình chữ nhật)
△ OAB = △ OCD (c.g.c) ⇒ S O A B = S O C D (1)
△ OAD = △ OBC (c.g.c) ⇒ S O A D = S O B C (2)
Kẻ AH ⊥ BD
S O A D = 1/2 AH.OD
S O A B = 1/2 AH.OB
Suy ra: S O A D = S O A B (3)
Từ (1), (2) và (3) ⇒ S O A B = S O B C = S O C D = S O D A