Chọn đáp án D

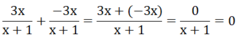
ĐK: x#0; x#-1

\(\frac{x^4}{1-x}\)+ x³ + x^{2 + 1}

^{= \(\frac{x^4}{1-x}\)}+ \(\frac{x^3\left(1-x\right)}{1-x}\)+ \(\frac{x^2\left(1-x\right)}{1-x}\)+ \(\frac{1-x}{1-x}\)

= \(\frac{x^4+x^3-x^4+x^2-x^3+1-x}{1-x}\)

= \(\frac{x+1}{1-x}\)

- Muốn cộng hai phân thức cùng mẫu, ta cộng các tử với nhau và giữ nguyên mẫu.

- Muốn cộng hai phân thức khác mẫu, ta quy đồng mẫu thức rồi cộng các phân thức cùng mẫu vừa tìm được.

\(\dfrac{3x}{x^3-1}+\dfrac{x-1}{x^2+x+1}\)

\(=\dfrac{3x}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{\left(x-1\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)

\(=\dfrac{3x+x^2-2x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)

\(=\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)

\(=\dfrac{1}{x-1}\)

Chọn đáp án B

Bài 1: 

a: \(\dfrac{25}{42}-\dfrac{20}{63}=\dfrac{75-40}{126}=\dfrac{35}{126}=\dfrac{5}{18}\)

b: \(\dfrac{9}{20}-\dfrac{13}{75}-\dfrac{1}{6}=\dfrac{135}{300}-\dfrac{52}{300}-\dfrac{50}{300}=\dfrac{33}{300}=\dfrac{11}{100}\)

a) \(\frac{1}{x^2-x+1}+1-\frac{x^2+2}{x^3+1}\)

+) Đkxđ: \(\hept{\begin{cases}x^2-x+1\ne0\\x^3+1\ne0\end{cases}\Leftrightarrow\hept{\begin{cases}x^2-2.x.\frac{1}{2}+\left(\frac{1}{2}\right)^2+\frac{3}{4}\ne0\\x^3\ne-1\end{cases}\Leftrightarrow}\hept{\begin{cases}\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ne0\left(lđ\right)\\x\ne-1\end{cases}}}\)

+) \(A=\frac{1}{x^2-x+1}+1-\frac{x^2+2}{x^3+1}\)

\(=\frac{1}{x^2-x+1}+1-\frac{x^2+2}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\frac{x+1+x^3+1-x^2+2}{\left(x+1\right)\left(x^2-x+1\right)}\)

\(=\frac{x^3-x^2+x+4}{\left(x+1\right)\left(x^2-x+1\right)}\)

P/s: ko chắc

Huhu luoi qua

a) \(\frac{1}{x^2-x+1}+1-\frac{x^2+2}{x^3+1}\)

\(=\frac{1}{x^2-x+1}+1-\left(\frac{x^2+2}{x^3+1}\right)\)

\(=\frac{x^5-2x^4+3x^3-2x^2+x}{x^5-x^4+x^3+x^2-x+1}\)

\(=\frac{x\left(x^4-2x^3+3x^2-2x+1\right)}{\left(x+1\right)\left(x^4-2x^3+3x^2-2x+1\right)}\)

\(=\frac{x}{x+1}\)

b) \(\frac{7}{x}-\frac{x}{x+6}+\frac{36}{x^2+6x}\)

\(=\frac{-x^2+7x+78}{x^2+6x}\)

\(=\frac{\left(-x-6\right)\left(x-13\right)}{x\left(x+6\right)}\)

\(=\frac{-x+13}{x}\)