Giải bất phương trình - 4x – 8 < 0 và biểu diễn tập nghiệm trên trục số.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 5 2017
Ta có: 4x – 8 ≥ 3(3x – 2) + 4 – 2x
⇔ 4x – 8 ≥ 9x – 6 + 4 – 2x
⇔ 4x – 9x + 2x ≥ - 6 + 4 + 8
⇔ -3x ≥ 6
⇔ x ≤ -2
Vậy tập nghiệm của bất phương trình là {x|x ≤ -2}
27 tháng 6 2016
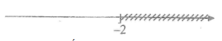
\(x^2-4x+3\ge0\)
\(\left(x-1\right)\left(x-3\right)\ge0\)
TH1; X-1>=0 VA X-3>=0
TH2: X-1=<0 VA X-3<=0
Vay x>=3 hoac x<=1
PT
1
CM
17 tháng 6 2017
2x – 3 > 0
⇔ 2x > 3 (Chuyển vế -3).
⇔ 
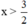(Chia cả hai vế cho 2 > 0, BĐT không đổi chiều).
Vậy BPT có nghiệm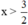 
PT
1
CM
12 tháng 10 2017
3x + 4 < 0
⇔ 3x < -4 (chuyển vế 4).
⇔ 
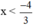(Chia cả hai vế cho 3 > 0).
Vậy BPT có tập nghiệm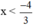 
PT
1
CM
6 tháng 11 2017
4 – 3x ≤ 0
⇔ -3x ≤ -4 (Chuyển vế hạng tử 4).
⇔ 
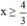(Chia cả hai vế cho -3 < 0, BPT đổi chiều).
Vậy BPT có tập nghiệm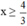 
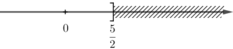
PT
1
CM
29 tháng 12 2018
5 – 2x ≥ 0
⇔ -2x ≥ -5 (Chuyển vế hạng tử 5).
⇔ 
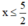(Chia cả hai vế cho -2 < 0, BĐT đổi chiều).
Vậy BPT có nghiệm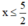 
-4x – 8 < 0 ⇔ -4x < 8
⇔ -4x : (- 4) > 8: (- 4) ⇔ x > -2
Vậy tập nghiệm của bất phương trình -4x – 8 < 0 là {x|x > -2}
Biểu diễn trên trục số