Tìm tập xác định của các hàm số y = tan x + c o t x 1 - sin 2 x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Biểu thức \(\frac{{1 - \cos x}}{{\sin x}}\) có nghĩa khi \(\sin x \ne 0\), tức là \(x \ne k\pi \;\left( {k\; \in \;\mathbb{Z}} \right)\).
Vậy tập xác định của hàm số đã cho là \(\mathbb{R}/{\rm{\{ }}k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}\} \;\)
b) Biểu thức \(\sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} \) có nghĩa khi \(\left\{ {\begin{array}{*{20}{c}}{\frac{{1 + \cos x}}{{2 - \cos x}} \ge 0}\\{2 - \cos x \ne 0}\end{array}} \right.\)
Vì \( - 1 \le \cos x \le 1 ,\forall x \in \mathbb{R}\)
Vậy tập xác định của hàm số là \(D = \mathbb{R}\)

ĐKXĐ:
a. Không hiểu đề bài là gì
b. \(3-2cosx\ge0\)
\(\Leftrightarrow cosx\le\dfrac{3}{2}\) (luôn đúng)
Vậy \(D=R\)
c. \(\left\{{}\begin{matrix}\dfrac{1+cosx}{1-cosx}\ge0\left(luôn-đúng\right)\\1-cosx\ne0\end{matrix}\right.\)
\(\Leftrightarrow cosx\ne1\Leftrightarrow x\ne k2\pi\)

Biểu thức \(\frac{1}{{\sin x}}\) có nghĩa khi \(\sin x \ne 0\), tức là \(x \ne k\pi \;\left( {k\; \in \;\mathbb{Z}} \right)\).
Vậy tập xác định của hàm số đã cho là \(\mathbb{R}/{\rm{\{ }}k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}\} \;\)

a) \(D=R\backslash\left\{1\right\}\)
b) \(y\left(x\right)\) xác định khi:
\(cos\dfrac{x}{3}\ne0\Leftrightarrow\dfrac{x}{3}\ne\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x\ne\dfrac{3\pi}{2}+k3\pi\)
\(D=R\backslash\left\{\dfrac{3\pi}{2}+k3\pi\right\};k\in Z\)
c) \(y\left(x\right)\) xác định khi:
\(sin2x\ne0\Leftrightarrow2x\ne k\pi\)\(\Leftrightarrow x\ne\dfrac{k\pi}{2}\).
\(D=R\backslash\left\{\dfrac{k\pi}{2}\right\};k\in Z\)
d) \(y\left(x\right)\) xác định khi:
\(x^2-1\ne0\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ne-1\end{matrix}\right.\).
\(D=R\backslash\left\{1;-1\right\}\)
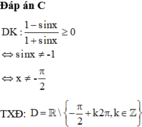
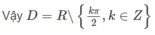
Điều kiện: cosx ≠ 0; sinx ≠ 0 và sin2x ≠ 1.
⇔ x ≠ kπ/2, k ∈ Z và x ≠ π/4 + kπ, k ∈ Z.
Vậy tập xác định của hàm số là
D \ R [(kπ/2,k ∈ Z)] ∪ [(π/4 + kπ,k ∈ Z)].