Cho 2 x 2 - 3 x + 5 x - 3 ' = a x 2 - b x + c ( x - 3 ) 2 Tính S=a+2b+3c
A. – 18
B. 38
C. – 6
D. 20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

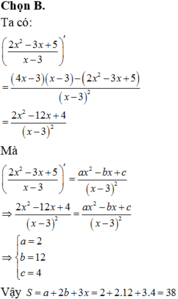

\(\begin{array}{l}A + B + C\\ = (3{x^4} - 2{x^3} - x + 1) + ( - 2{x^3} + 4{x^2} + 5x) + ( - 3{x^4} + 2{x^2} + 5)\\ = 3{x^4} - 2{x^3} - x + 1 - 2{x^3} + 4{x^2} + 5x - 3{x^4} + 2{x^2} + 5\\ = (3{x^4} - 3{x^4}) + ( - 2{x^3} - 2{x^3}) + (4{x^2} + 2{x^2}) + ( - x + 5x) + (1 + 5)\\ = 0 + ( - 4{x^3}) + 6{x^2} + 4x + 6\\ = - 4{x^3} + 6{x^2} + 4x + 6\\A - B + C\\ = (3{x^4} - 2{x^3} - x + 1) - ( - 2{x^3} + 4{x^2} + 5x) + ( - 3{x^4} + 2{x^2} + 5)\\ = 3{x^4} - 2{x^3} - x + 1 + 2{x^3} - 4{x^2} - 5x - 3{x^4} + 2{x^2} + 5\\ = (3{x^4} - 3{x^4}) + ( - 2{x^3} + 2{x^3}) + ( - 4{x^2} + 2{x^2}) + ( - x - 5x) + (1 + 5)\\ = 0 + 0 + ( - 2{x^2}) - 6x + 6\\ = - 2{x^2} - 6x + 6\\A - B - C\\ = (3{x^4} - 2{x^3} - x + 1) - ( - 2{x^3} + 4{x^2} + 5x) - ( - 3{x^4} + 2{x^2} + 5)\\ = 3{x^4} - 2{x^3} - x + 1 + 2{x^3} - 4{x^2} - 5x + 3{x^4} - 2{x^2} - 5\\ = (3{x^4} + 3{x^4}) + ( - 2{x^3} + 2{x^3}) + ( - 4{x^2} - 2{x^2}) + ( - x - 5x) + (1 - 5)\\ = 6{x^4} + 0 + ( - 6{x^2}) - 6x + ( - 4)\\ = 6{x^4} - 6{x^2} - 6x - 4\end{array}\)

a)
A=\(x^2+y^2=\left(x^2+2xy+y^2\right)-2xy=\left(x+y\right)^2-2xy=a^2-2b\)
\(B=x^3+y^3=\left(x^3+3x^2y+3xy^2+y^3\right)-3x^2y-3xy^2=\left(x+y\right)^3-3xy\left(x+y\right)=a^3-3ab\)
\(C=x^5+y^5=\left(x^5+y^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4\right)-5x^4y-10x^3y^2-10x^2y^3-5xy^4\)
\(=\left(x+y\right)^5-5xy\left(x^3+2xy^2+2x^2y+y^3\right)=\left(x+y\right)^5-5xy\left(x^3+3xy^2+3x^2y+y^3-xy^2-x^2y\right)\)
\(=\left(x+y\right)^5-5xy\left(\left(x+y\right)^3-xy\left(x+y\right)\right)=a^5-5b\left(a^3-ab\right)\)

bài 2 nè
a+b+c = 0
=>(a+b+c)^3 = 0
a^3 + b^3 + c^3 + 3(a+b)(b+c)(a+c) = 0
vì a+b = -c
a+c = -b
b+c = -a
thay vào => a^3 + b^3 + c^3 - 3abc = 0
=> a^3 + b^3 + c^3 = 3abc

Bài 4:
a: \(\Leftrightarrow x^3-3x^2+3x-1-x^3-27+3x^2-12=2\)
\(\Leftrightarrow3x-40=2\)
=>3x=42
hay x=14
b: \(\Leftrightarrow x^3+8-x^3-2x=0\)
=>-2x+8=0
=>-2x=-8
hay x=4
c: \(x\left(x-2\right)+\left(x-2\right)=0\)
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
d: \(5x\left(x-3\right)-x+3=0\)
=>5x(x-3)-(x-3)=0
=>(x-3)(5x-1)=0
=>x=3 hoặc x=1/5
e: \(3x\left(x-5\right)-\left(x-1\right)\left(3x+2\right)=30\)
\(\Leftrightarrow3x^2-15x-3x^2-2x+3x+2=30\)
=>-14x=28
hay x=-2
f: \(\Leftrightarrow\left(x+2\right)\left(x+30-x-5\right)=0\)
=>x+2=0
hay x=-2