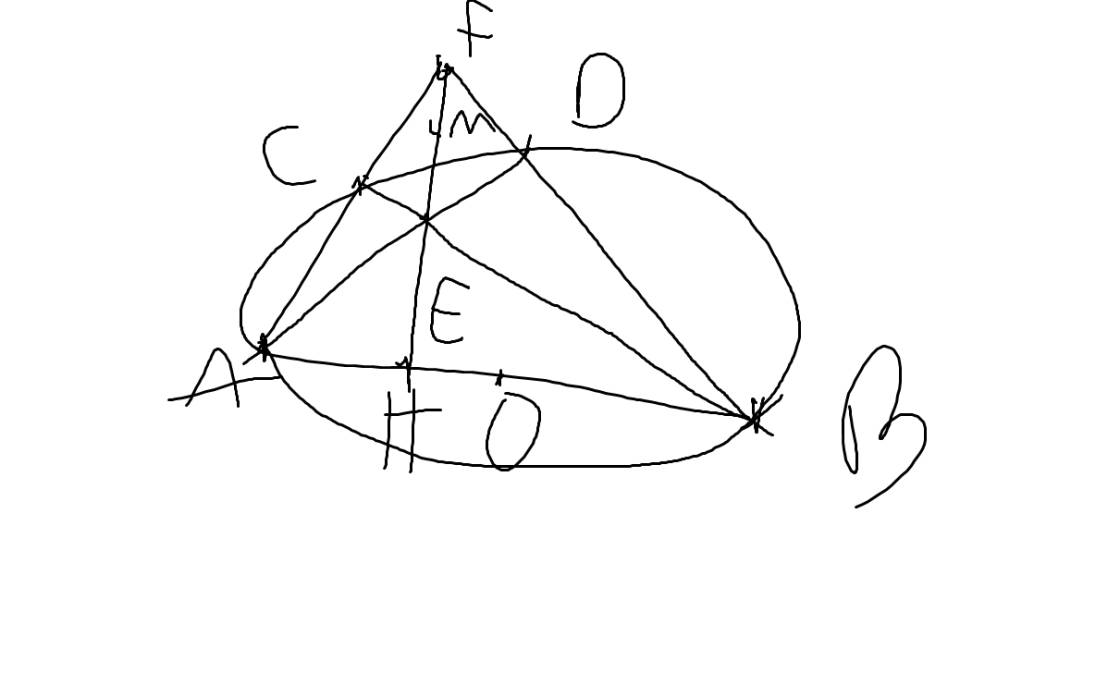
Nhanh nhanh mn ơi, cứu t vs chỉ t cái lệnh để vẽ hình này đi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(ĐK:x\ne0\)
\(\dfrac{x-1}{3}+\dfrac{x+3}{x}=2\)
\(\Leftrightarrow\dfrac{x\left(x-1\right)+3\left(x+3\right)}{3x}=\dfrac{6x}{3x}\)
\(\Leftrightarrow x\left(x-1\right)+3\left(x+3\right)=6x\)
\(\Leftrightarrow x^2-x+3x+9-6x=0\)
\(\Leftrightarrow x^2-4x+9=0\)
Ta có: \(x^2-4x+9=x^2-4x+4+5=\left(x-2\right)^2+5\ge5>0\)
Vậy pt vô nghiệm

\(P=\left(\dfrac{x^2+1}{x^2-9}-\dfrac{x}{x+3}+\dfrac{5}{3-x}\right):\left(\dfrac{2x+10}{x+3}-1\right)\)
\(=\left(\dfrac{x^2+1}{\left(x-3\right)\left(x+3\right)}-\dfrac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-\dfrac{5\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{2x+10}{x+3}-\dfrac{x+3}{x+3}\right)\)
\(=\left(\dfrac{x^2+1-x^2+3x-5x-15}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{2x+10-x-3}{x+3}\right)\)
\(=\left(\dfrac{-2x-14}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{x+7}{x+3}\right)\)
\(=\dfrac{-2\left(x+7\right)}{\left(x-3\right)\left(x+3\right)}.\dfrac{x+3}{x+7}\)
\(=\dfrac{-2}{x-3}\)
đk : x khác -3 ; 3 ; -7
\(P=\left(\dfrac{x^2+1+x\left(x-3\right)+5x+15}{x^2-9}\right):\left(\dfrac{2x+10-x-3}{x+3}\right)\)
\(=\dfrac{2x^2+1+2x+15}{x^2-9}:\dfrac{x+7}{x+3}=\dfrac{2x^2+2x+16}{\left(x-3\right)\left(x+7\right)}\)

Lời giải:
$x^2+2xy+6x+6y+2y^2+8=0$
$\Leftrightarrow (x^2+2xy+y^2)+6x+6y+y^2+8=0$
$\Leftrightarrow (x+y)^2+6(x+y)+y^2+8=0$
$\Leftrightarrow (x+y+3)^2+y^2-1=0$
$\Leftrightarrow (x+y+3)^2=1-y^2\leq 1$
$\Rightarrow -1\leq x+y+3\leq 1$
$\Rightarrow -4\leq x+y\leq -2$
$\Rightarrow 2020\leq x+y+2024\leq 2022$
Vậy $P_{\min}=2020; P_{\max}=2022$

\(=\dfrac{-5}{12}+\dfrac{6}{11}+\dfrac{7}{17}+\dfrac{5}{11}+\dfrac{5}{12}=1+\dfrac{7}{17}=\dfrac{24}{17}\)

a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB\(\perp\)AF tại C
Xét tứ giác BHCF có \(\widehat{BHF}=\widehat{BCF}=90^0\)
nên BHCF là tứ giác nội tiếp
=>B,H,C,F cùng thuộc một đường tròn
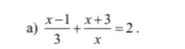
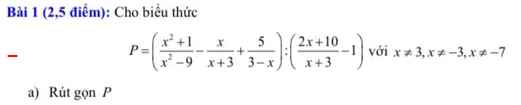
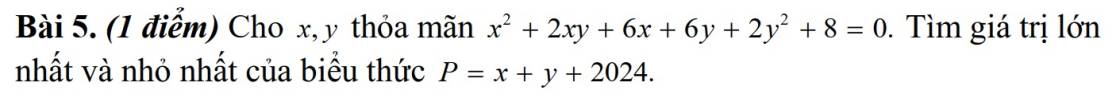 cứu t mn, nhanh nha sáng mai tui đi học rùi chậm nhất là 12h
cứu t mn, nhanh nha sáng mai tui đi học rùi chậm nhất là 12h

là sao ạ?
mình ko hiểu
?