Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x=1 và x=4, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x ( 1 ≤ x ≤ 4 ) thì được thiết diện là một hình lục giác đều có độ dài cạnh là 2x.
![]()
![]()
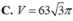
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
V = ∫ 1 3 3 x 3 x 2 − 2 d x = 1 3 [ ( 3 x 2 − 2 ) 3 2 ] 3 1 = 124 3

Đáp án C
Diện tích thiết diện là S = 2 x 2 x 2 − 1 .
Vậy thể tích V của vật là
V = 1 2 2 x 2 x 2 − 1 d x .
Đặt
u = 2 x 2 − 1 ⇒ d u = 2 x 2 x 2 − 1 d x ⇒ d x = u d u 2 x .
Vậy V = ∫ 1 7 u 2 d u = u 3 3 1 7 = 7 7 − 1 3 .

Ta có diện tích thiết diện là
S ( x ) = 1 2 πR 2 = 1 2 πx 2 4 - x = 1 2 π 4 x 2 - x 3
Thể tích của vật thể cần tìm là
V = ∫ 0 4 S ( x ) d x = 1 2 π ∫ 0 4 4 x 2 - x 3 dx = 1 2 π 4 3 x 3 - 1 4 x 4 | 0 4 = 32 π 3
Chọn đáp án D.

Chọn: D
Ta có diện tích thiết diện là
![]()
Thể tích của vật thể cần tìm là
![]()

Chọn B