Cho số phức z = - 2 i - 1 . Điểm biểu diễn số phức liên hợp của z trong mặt phẳng phức là:
A. M(-1;-2).
B. M(2;-1).
C. M(-2;1).
D. M(-1;2).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Ta có: z = - 2i – 1 = -1 - 2i
Số phức liên hợp của z là ![]() có phần thực là -1, phần ảo là 2.
có phần thực là -1, phần ảo là 2.
Vậy điểm biểu diễn số phức liên hợp là M(-1;2)

Đáp án A.
Số phức liên hợp của z = 1 − 2 i là z ¯ = 1 + 2 i .
Do đó M 1 1 ; 2 là điểm biểu diễn của z ¯ .

Chọn A.
Gọi M(x; y) , F1= ( -2; 0) và F2( 2; 0).
Ta có |z + 2| + |z – 2| = 8 ![]()
Hay MF1+ MF2 = 8.
Do đó điểm M(x; y) nằm trên elip (E ) có 2a = 8 nên a = 4
ta có F1F2 = 2c nên 4 = 2c hay c = 2
Ta có b2 = a2 - c2 = 16 - 4 = 12
Vậy tập hợp các điểm M là elip 

Chọn A.
Ta có : 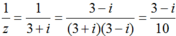
Do đó điểm biểu diễn số phức 1/z trong mặt phẳng phức là: 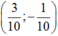
Chọn D.
Số phức liên hợp của z là z ¯ = - 1 + 2 i có phần thực là -1, phần ảo là 2.
Vậy điểm biểu diễn số phức liên hợp là M(-1;2)