Xét các số thực a, b thỏa mãn 1 4 < b < a < 1 Biểu thức P = log a ( b - 1 4 ) - log a b b đạt giá trị nhỏ nhất khi
A. log a b = 1 3
B. log a b = 2 3
C. log a b = 3 2
D. log a b = 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

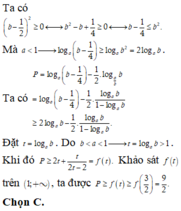

Ta có:
\(\left(b-\dfrac{1}{2}\right)^2\ge0\) <=> \(b^2-b+\dfrac{1}{4}\ge0\) <=>\(b-\dfrac{1}{4}\le b^2\)
Mà :
a<1 => \(log_a\left(b-\dfrac{1}{4}\right)\ge log_ab^2=2log_ab\)
P=\(log_a\left(b-\dfrac{1}{4}\right)-\dfrac{1}{2}log_{\dfrac{a}{b}}b=log_a\left(b-\dfrac{1}{4}\right)-\dfrac{1}{2}.\dfrac{log_ab}{1-log_ab}\ge2log_ab-\dfrac{1}{2}.\dfrac{log_ab}{1-log_ab}\)
Đặt t=logab
Do b<a<1 => t=logab >1
Khi đó \(P\ge2t+\dfrac{t}{2t-2}=f\left(t\right)\). Khảo sát f(t) trên (1;+\(\infty\)) ta đc
P\(\ge\)f(t) \(\ge\) f\(\left(\dfrac{3}{2}\right)\) = \(\dfrac{9}{2}\)

Ta có:
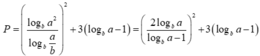
Đặt t= logba-1 > logbb -1=0 ,
khi đó:
P = 2 t + 2 t 2 + 3 t = f ( t ) f ' t = 2 . 2 t + 2 t . - 2 t 2 + 3 = 3 t 3 - 8 ( t + 1 ) t 3
F’ (t) =0 khi 3t3-8( t+1) =0 hay t= 2.
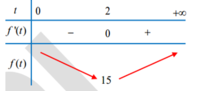
Suy ra Pmin =f(2) =15
Chọn D.