Đáp án là B

Đáp án là D

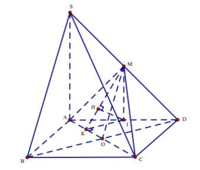
+ Gọi O là giao điểm của AC,BD

⇒ MO \\ SB ⇒ SB \\ ACM

⇒ d  SB,ACM = d B,ACM = d D,ACM  .

+ Gọi I là trung điểm của AD ,

M I \ \ S A ⇒ M I ⊥ A B C D d     D , A C M     = 2 d     I , A C M  .

+ Trong ABCD: IK ⊥ AC  (với K  ∈ AC ).

+ Trong MIK: IH ⊥ MK  (với H ∈ MK ) (1)  .

+ Ta có: AC ⊥  MI ,AC ⊥  IK ⇒  AC ⊥  MIK

  ⇒  AC ⊥  IH (2) .

Từ 1 và 2 suy ra

IH ⊥  ACM ⇒  d  I ,ACM  = IH  .

+ Tính IH ?

- Trong tam giác vuông MIK. : I H = I M . I K I M 2 + I K 2 .

- Mặt khác: M I = S A 2 = a , I K = O D 2 = B D 4 = a 2 4

⇒ I H = a a 2 4 a 2 + a 2 8 = a 3

Vậy   d     S B , A C M = 2 a 3 .

Lời giải khác

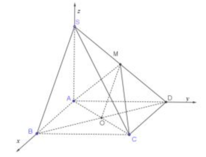
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=45^0\Rightarrow AC=SA=a\sqrt{2}\)

\(\Rightarrow AB=a\)

Gọi N là trung điểm SA \(\Rightarrow NM||SB\Rightarrow SB||\left(DMN\right)\)

\(\Rightarrow d\left(DM;SB\right)=d\left(SB;\left(DMN\right)\right)=d\left(B;\left(DMN\right)\right)\)

Mà M là trung điểm AB \(\Rightarrow d\left(B;\left(DMN\right)\right)=d\left(A;\left(DMN\right)\right)\)

Từ A kẻ AH vuông góc DM \(\Rightarrow DM\perp\left(NAH\right)\)

Trong mp (NAH), từ A kẻ \(AK\perp NH\Rightarrow AK=d\left(A;\left(DMN\right)\right)\)

\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AM.AD}{\sqrt{AM^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)

\(\dfrac{1}{AK^2}=\dfrac{1}{AN^2}+\dfrac{1}{AH^2}\Rightarrow AK=\dfrac{AN.AH}{\sqrt{AN^2+AH^2}}=\dfrac{a\sqrt{7}}{7}\)

Đáp án C

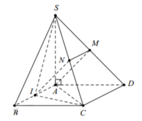
Gọi I;N lần lượt là trung điểm của AB   và  SC

Suy ra AMNI   là hình bình hành   ⇒ A M ∥ I N ⇒ A M ∥ S C I

Do đó   d A M , S C = d A M , S C I = d A ; S C I = h

Kẻ   A H ⊥ I C    H ∈ I C ,   A K ⊥ S H    K ∈ S H ⇒ A K ⊥ S C I

Ta có   S Δ A C I = 1 2 S Δ A B C = 1 2 . A H . I C ⇒ A H = a 2 4 : a 5 4 = a 5 5

Tam giác SAH  vuông tại A , có   1 A K 2 = 1 A H 2 + 1 S A 2 ⇒ A K = 2 a 21

Vậy khoảng cách cần tính là   h = 2 a 21 21

Đáp án D

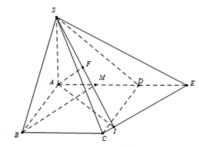
Dựng C E / / B M  khi đó d B M ; S C = d B M ; S C E  

Ta có A E M E = 3 2 ⇒ d M = 2 3 d A  

Dựng A I ⊥ C E ; A F ⊥ S I ⇒ d A = A F  

Trong đó S A = a , A I = A E sin E ,  với

sin E = C D C E = a a 2 + a 2 2 = 2 5 ⇒ A I = 3 a 2 . 2 5 = 3 a 5  

Hoặc tính  A I = 2 S A C D C D ⇒ d A = A I . S A A I 2 + S A 2 = 3 14 ⇒ d M = 2 14

Đáp án D

Chọn hệ trục tọa độ như hình vẽ