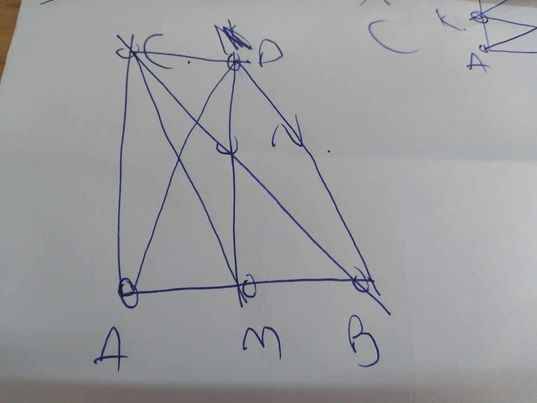
cho tam giác ABC, các điểm M, N, P lần lượt là trung điểm của cách cạnh AB, AC, BC. Trên tia đối của tia NP lấy điểm D sao cho ND=NP.
a)Chứng minh: tứ giác ADCP là hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 11 2021
a: Xét tứ giác ADCP có
N là trung điểm của AC
N là trung điểm của DP
Do đó: ADCP là hình bình hành
7 tháng 11 2021
a: Xét tứ giác ADCP có
N là trung điểm của AC
N là trung điểm của DP
Do đó: ADCP là hình bình hành
15 tháng 11 2021
a: Xét tứ giác ADCP có
N là trung điểm của AC
N là trung điểm của DP
Do đó: ADCP là hình bình hành
27 tháng 10 2021
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra:MN//BC
hay BMNC là hình thang
7 tháng 11 2021
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: BC=2MN
hay BC=6(cm)
17 tháng 12 2023
a: Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{BC}{2}\)
Ta có: MN//BC
D\(\in\)NM
Do đó; MD//CB
ta có: \(MN=\dfrac{CB}{2}\)
\(MN=\dfrac{MD}{2}\)
Do đó:CB=MD
Xét tứ giác BMDC có
BC//MD
BC=MD
Do đó: BMDC là hình bình hành
b: Xét tứ giác AMCD có
N là trung điểm chung của AC và MD
nên AMCD là hình bình hành
29 tháng 12 2023
Sửa đề: MN=MP
a: Xét tứ giác ANBP có
M là trung điểm chung của AB và NP
=>ANBP là hình bình hành
b: Ta có: ANBP là hình bình hành
=>AP//NB và AP=NB
Ta có: AP//NB
N\(\in\)BC
Do đó: AP//NC
Ta có: AP=NB
NB=NC
Do đó: AP=NC
Xét tứ giác APNC có
AP//NC
AP=NC
Do đó: APNC là hình bình hành
=>AC=NP
AH
Akai Haruma
Giáo viên
27 tháng 12 2023
Tia đối của MN có điểm P thì $NP>MN$ bạn nhé. Bạn xem lại đề.
3 tháng 1
a: Xét tứ giác BMCD có
N là trung điểm chung của BC và MD
=>BMCD là hình bình hành
b: Ta có: BMCD là hình bình hành
=>BM//CD và BM=CD
Ta có: BM//CD
M\(\in\)AB
Do đó: AM//CD
ta có: BM=CD
AM=MB
Do đó: AM=CD
Xét tứ giác AMDC có
AM//DC
AM=DC
Do đó: AMDC là hình bình hành
Hình bình hành AMDC có \(\widehat{MAC}=90^0\)
nên AMDC là hình chữ nhật
c: Ta có: AMDC là hình chữ nhật
=>\(\widehat{DMA}=90^0\)
=>DM\(\perp\)AB tại M
Xét ΔDBA có
DM là đường cao
DM là đường trung tuyến
Do đó: ΔDBA cân tại D
a: Xét tứ giác APCD có
N là trung điểm của AC
N là trung điểm của PD
Do đó: APCD là hình bình hành