Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm các tam giác ABC và ABD. Trong các mệnh đề sau, mệnh đề nào đúng?
A. IJ//AB
B. IJ // DC
C. IJ//BD
D. IJ//AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
11 tháng 5 2018
Đúng(0)
Những câu hỏi liên quan
CM
18 tháng 2 2017
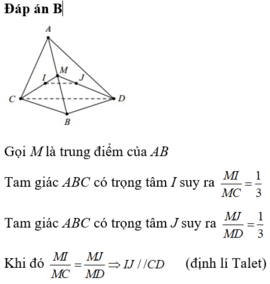
Đáp án B
Gọi M là trung điểm của AB
Tam giác ABC có trọng tâm I suy ra M I M C = 1 3
Tam giác ABC có trọng tâm J suy ra M J M D = 1 3
Khi đó M I M C = M J M D ⇒ I J / / C D (định lí Talet)
PT
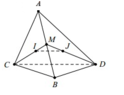
Cho tứ diện ABCD có I và J lần lượt là trọng tâm các tam giác ABC và ABD. Chứng minh rằng: IJ // CD.
1
CM
24 tháng 3 2019
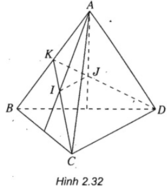
Gọi K là trung điểm của AB.
Vì I là trọng tâm của tam giác ABC nên I ∈ KC và vì J là trọng tâm của tam giác ABD nên J ∈ KD.
Từ đó suy ra
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2021
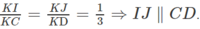
Câu b đề bài thiếu, tìm giao tuyến của mặt nào và (ABD) vậy em?
CM
22 tháng 4 2018
Đáp án A
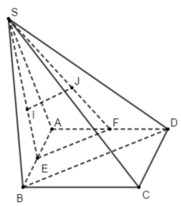
Tam giác SAB có I là trọng tâm và E là trung điểm của AB
Nên ta có S I S E = 2 3 (1)
Tam giác SAD có J là trọng tâm và F là trung điểm của AD
Nên ta có S J S F = 2 3 (2)
Từ (1) và (2) ta có: IJ // EF (3) (định lý Ta-lét trong tam giác SEF)
Tam giác ABD có EF là đường trung bình nên EF // BD (4)
Từ (3) và (4) suy ra IJ // BD
Mà BD (SBD)
Do đó IJ // (SBD).