Với ba điểm A, B, C phân biệt.Khi A nằm giữa B, C thì hai vecto  A B → ;     A C → ngược hướng nên 

điều kiện cần và đủ để ba điểm A, B, C thẳng hàng và A nằm giữa B, C là:  ∃ k   <   0 :   A B →   =   k A C →

Đáp án A

Giao điểm của AB và CD chính là điểm M thỏa mãn đề bài.

Một lẽ dĩ nhiên là nếu AB song song với CD thì ta không thể tìm được giao điểm của chúng, dẫn đến không tìm được điểm M theo yêu cầu.

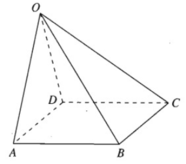
Giả sử bốn điểm A, B, C, D tạo thành một hình bình hành ta có:

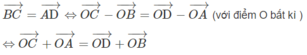
Ngược lại, giả sử ta có hệ thức:

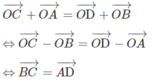
Vì A, B, C, D không thẳng hàng nên tứ giác ABCD là hình bình hành.

P là giao điểm của đường thẳng OA và đường thẳng BQ.

khó thế

Tính tổng các số nguyên x biết :

1, -20<x<21

2, -18< -x<- 17

3,-27<x<-27

4, |x|<-3

5, |-x|<5

Mọi người giúp mình với                                         HELP ME

Chọn B 

Tham khảo:

a)  \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}AB//AM\\B \; \text {và}\;  M \; \text {nằm cùng phía so với điểm A}\end{array} \right.\)

\( \Leftrightarrow \) A, B, thẳng hàng và A nằm giữa B và M

b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương

TH1: \(MA < MB\)

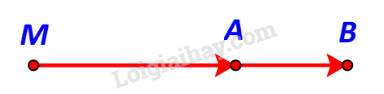
 M, A, B thẳng hàng & A nằm giữa M và B.

TH2: \(MA > MB\)

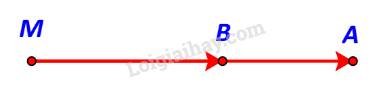
M, A, B thẳng hàng & B nằm giữa M và A.

c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng

TH1: \(AM < AB\)

A, M, B thẳng hàng & M nằm giữa A và B.

TH2: \(AB < AM\)

A, M, B thẳng hàng & B nằm giữa A và M.

d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}MA//MB\\A \; \text {và} \; B\; \text {nằm về hai phía so với điểm M}\end{array} \right.\)

\( \Leftrightarrow \) A, M, B thẳng hàng & M nằm giữa A và B.

Vậy điều kiện cần và đủ để M nằm giữa A và B là d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng

Đáp án B

Phương pháp:

+) Tìm điều kiện để phương trình y’ = 0 có hai nghiệm phân biệt thỏa mãn ĐKXĐ.

+) Viết phương trình đường thẳng AB. Để A, B, C thẳng hàng ó C ∈ AB

Cách giải: TXĐ: D = R\{|m|}

Ta có:

<=> 

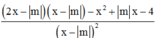
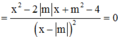
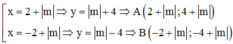
=> Đồ thị hàm số luôn có hai điểm cực trị A, B phân biệt.

Đường thẳng AB có phương trình:

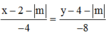
Để A, B, C(4;2) phân biệt thẳng hàng ó CAB => 2 = 4.2 - |m| ó |m| = 6  

Khi đó ta có: B(4;2) ≡ C => không thỏa mãn.

Vậy không có giá trị nào của m thỏa mãn yêu cầu bài toán