chứng minh đó, bọn bây đui hết rồi ak, đừng ns kết quả ra nữa, ttốn giấy mực olm, đứa nào ko lm ra thì biến

a) \(\Delta\)AEF=\(\Delta\)ECD ( g-c-g) => EF= CD ; DE = AF

  \(\Delta\)BFD = \(\Delta\)EDF ( g-c-g) => BF = DE ; BD = EF

=> AF = BE ; BD=CD => dpcm

b) theo a) => DF là đường TB của \(\Delta\) ABC => dpcm

vẽ hinh sau đó mới tính

mún trừ điểm ak làm gì thế

a) TA CÓ :EF//AB

suy ra : góc AEF=gócECD     (1)

            ED // AB           

suy ra :gócCED =gócEAF         (2)

TA CÓ :AE = EC (gt)              (3)

từ 1,2,3 suy ra tam giác FAE=DEC

suy ra AF=ED (4) và EF=DC (5)

theo bai ta co :ED//AB  mà Fthuộc AB nên ED//FB

                      EF//BC mà Dthuộc BCnên EF//BD

từ trên ta suy ra EFBD là hinh bình hành

suy ra BF=ED (6) và EF=BD (7)

từ 4,6 suy ra AF =BF hay Flà trung điểm của AB

Từ 5,7 suy ra BD=DC hay Dlà trung điểm của BC 

b) ta có :AF=DE (câu a) và AF//ED 

nên suy ra :AFDE là hình bình hành 

suy ra FD//AE (đpcm)   và FD=AE

mà AE=EC=1/2AC 

nên FD=1/2AC (đpcm)

***tick cho mik nhé **!!!

Cho tam giác ABC. Gọi E là trung điểm của AC. Đường thẳng qua E song song với BC cắt AB tại F. Đường thẳng qua E song song với AB cắt cạnh BC tại D.

a) Chứng minh: F là trung điểm của AB. D là trung điểm của BC.

b) Chứng minh: DF // AC ; DF = 1/2 AC

em mới lớp 5 à, honk làm đk! _ _|

đăng ít thui, đăng hoài chưa chắc có người giải đâu pn ak!!

a) Co E la trung diem cua AC, FE//BC suy ra F la trung diem AB(duong trung binh )

Co E la trung diem AC, ED//AB suy ra D la trung diem BC(duong trung binh)

b) Co F la trung diem AB (cmt), D la trung diem BC (cmt) suy ra FD la duong trung binh cua tam giac ABC

suy ra FD//=1/2 AC (t/c duong trung binh)

D là TĐ của AB mà DE //BC nên DE là đg TB của tam giác ABC -->E là TĐ của AC.

E là TĐ của AC mà EF //AB nên EF là đg TB của tam giác CAB--->F là TĐ của BC

TB là j

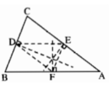
+)Xét tam giác BDF và ∆EFD có:

DF chung

∠BDF = ∠DFE ( hai góc so le trong; BC// EF)

∠BFD = ∠FDE ( hai góc so le trong; DE// AB)

Suy ra:∆ BDF = ∆EFD (g.c.g)

Suy ra BD = EF. Theo giả thiết, D là trung điểm của BC nên CD = DB = EF.

+) Xét ∆ CDE và ∆ EFA có :

CD = EF ( chứng minh trên)

∠(CDE) = ∠(EFA) = ∠(CBA)

∠(ECD) = ∠(AEF) (các góc đồng vị).

Suy ra: ∆ CDE = ∆ EFA ( g.c.g)

Suy ra CE = EA nên E là trung điểm của CD.