Cho a,b > 0 thỏa mãn a 2 + 4 b 2 = 12 a b . Xét hai mệnh đề sau
I : log 3 a + 2 b + 2 log 3 2 = 1 2 log 3 a + log 3 b I I : log 3 a + 2 b = 1 2 log 3 a + log 3 b
Mệnh đề nào là đúng trong các mệnh đề sau?
A. Chỉ (I)
B. Chỉ (II)
C. Cả hai sai
D. Cả hai đúng

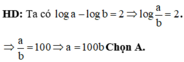
Ta có a 2 + 4 b 2 = 12 a b ⇔ a + 2 b 2 = 16 a b
Suy ra
2 log 3 a + 2 b = log 3 2 4 + log 3 a + log 3 b ⇔ log 3 a + 2 b = 2 log 3 2 + 1 2 log 3 a + log 3 b
Do đó cả hai mệnh đề đều sai
Đáp án C