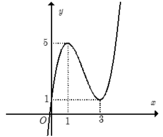
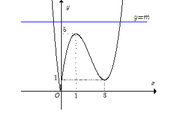
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?
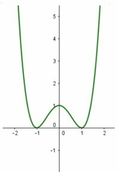
A. Phương trình f(x)=m luôn có nghiệm
B. Phương trình f(x)=m có hai nghiệm phân biệt nếu m=1
C. Phương trình f(x)=m có ít nhất hai nghiệm
D. Phương trình f(x)=0 có hai nghiệm phân biệt

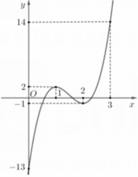


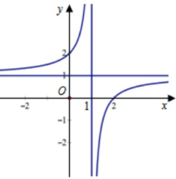
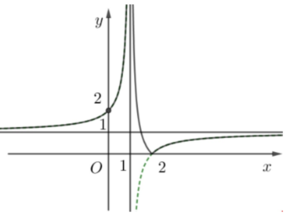
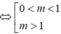
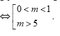
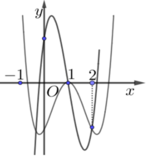
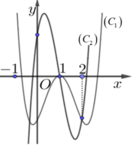




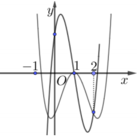
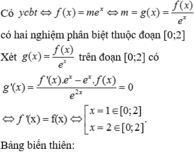
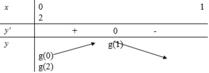

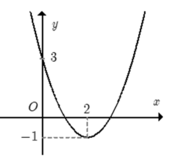
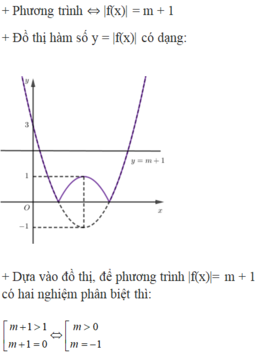
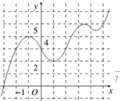
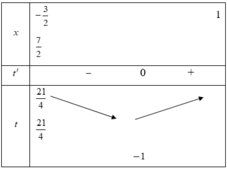
Đáp án D
Phương trình y=f(x) có hai nghiệm phân biệt