Tìm a để hàm số sau có giới hạn khi x → 2
f ( x ) = x 2 + a x + 2 khi x > 2 2 x 2 − x + 1 khi x ≤ 2
A. + ∞
B. − ∞
C. 1 2
D.1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Ta có:
![]() .
.![]()
Hàm số có giới hạn khi ![]()

Vậy a = 1/2 là giá trị cần tìm.

Chọn C.
Hàm số đã cho các định trên R \ {2}.
Ta có ![]()
Đặt 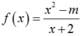 khi x < 3 (m là tham số, m > 0).
khi x < 3 (m là tham số, m > 0).
Ta có 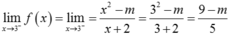 .
.
Để hàm số f(x) có giới hạn khi x → 3 thì 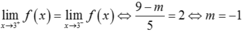 .
.

Chọn D.
Ta có: ![]()
![]()
Hàm số có giới hạn khi ![]()
⇔ a + 3 = 3a + 1 ⇔ a = 1.
Vậy a = 1 là giá trị cần tìm.

a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì, \({x_n} > - 1\) và \({x_n} \to - 1\). Khi đó \(f\left( {{x_n}} \right) = x_n^2 + 2\)
Ta có: \(\lim f\left( {{x_n}} \right) = \lim \left( {x_n^2 + 2} \right) = \lim x_n^2 + \lim 2 = {\left( { - 1} \right)^2} + 2 = 3\)
Vậy \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = 3\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì, \({x_n} < - 1\) và \({x_n} \to - 1\). Khi đó \(f\left( {{x_n}} \right) = 1 - 2{x_n}\).
Ta có: \(\lim f\left( {{x_n}} \right) = \lim \left( {1 - 2{x_n}} \right) = \lim 1 - \lim \left( {2{x_n}} \right) = \lim 1 - 2\lim {x_n} = 1 - 2.\left( { - 1} \right) = 3\)
Vậy \(\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) = 3\).
b) Vì \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ - }} {\rm{ }}f\left( x \right) = 3\) nên \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = 3\).
Chọn C.
Ta có:
lim x → 2 + f ( x ) = lim x → 2 + ( x 2 + a x + 2 ) = 2 a + 6 .
lim x → 2 − f ( x ) = lim x → 2 − ( 2 x 2 − x + 1 ) = 7 .
Hàm số có giới hạn khi x → 2 ⇔ lim x → 2 + f ( x ) = lim x → 2 − f ( x ) ⇔ 2 a + 6 = 7 ⇔ a = 1 2 .
Vậy a = 1 2 là giá trị cần tìm.