Cho biểu thức: A = sin2(a + b) – sin2a - sin2b. Đưa biểu thức trên về dạng tích:
A. A = 2cosa. sinb.sin( a + b)
B. A = 2.sina.cosb.cos(a + b)
C. A = 2cosa.cosb.cos(a + b)
D. A = 2sina.sinb.cos( a + b)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Sử dụng công thức hạ bậc và biến đổi tổng thành tích ta có :
A = sin2(a + b) – sin2a - sin2b
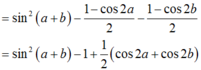
= -cos2(a + b) + cos( a + b) cos(a - b)
= cos (a +b) [ cos( a - b) – cos(a + b) ]
= 2 sina. sinb.cos(a + b)

\(P=sin^22a+cos^22a+sin^22b+cos^22b+2sin2a.sin2b+2cos2a.cos2b\)
\(P=2+2\left(sin2a.sin2b+cos2a.cos2b\right)=2+2cos\left(2a-2b\right)\)
\(P=2+2cos\frac{\pi}{3}=3\)

\(P=sin^2\left(a+b\right)-\frac{1}{2}+\frac{1}{2}cos2a-\frac{1}{2}+\frac{1}{2}cos2b\)
\(=sin^2\left(a+b\right)-1+\frac{1}{2}\left(cos2a+cos2b\right)\)
\(=-cos^2\left(a+b\right)+cos\left(a+b\right).cos\left(a-b\right)\)
\(=cos\left(a+b\right)\left[cos\left(a-b\right)-cos\left(a+b\right)\right]\)
\(=2sina.sinb.cos\left(a+b\right)\)

\(VT=\cos^2a-2.\dfrac{1}{2}\left[\cos\left(a+b\right)+\cos\left(a-b\right)\right].\cos\left(a+b\right)+\cos^2\left(a+b\right)=\)
\(=\cos^2a-\cos^2\left(a+b\right)-\cos\left(a+b\right)\cos\left(a-b\right)+\cos^2\left(a+b\right)=\)
\(=\cos^2a-\dfrac{1}{2}\left(\cos2a+\cos2b\right)=\)
\(=\dfrac{2\cos^2a-\cos^2a+\sin^2a-1+2\sin^2b}{2}=\)
\(=\dfrac{\left(\cos^2a+\sin^2a\right)-1+2\sin^2b}{2}=\sin^2b=VP\)
cos2a - cos (a+b) (2 cosa . cosb - cos (a+b) = sin2b
Cos2a - ( cos a.cosb- sina .sinb)( 2 cosa .cosb - ( cosa .cosb - sina .sinb) = sin2b
cos2a - (cosa.cosb - sina.sinb) (cosa.cosb + sina .sinb) = sin2b
cos2a - ( cos2a . cos2b - sin2a .sin2b = sin2b ) .
1 - sin2a - ( 1 - sin2a ) ( 1 - sin2b) - sin2a .sin2b = sin2b
1 - sin2a - ( 1- sin2b - sin2a + sin2a .sin2b - sin2 a .sin2b = sin2b
1 - sin2a -1 + sin2 b + sin2a = sin2b
Sin2b = Sin2b điều đã CM

Bài 1:
-Kiểu dữ liệu phù hợp là kiểu số thực (real)
Bài 2:
a) a*x*x*x+b*x*x+c*x+d
b) 1/(1+x)*(1+x)-2/(x*x+1)
Bài 3: (Lười quá, nhường bạn khác nhé :D)

a) \(=\sqrt{a}\left(\sqrt{a}-1\right)\)
b) \(=\left(\sqrt{a}\right)^2-2\sqrt{ab}+\left(\sqrt{b}\right)^2=\left(\sqrt{a}-\sqrt{b}\right)^2\)
c) \(=\left(\sqrt{x}\right)^2-2\sqrt{x}+1=\left(\sqrt{x}-1\right)^2\)
d) \(=\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)
e) \(=\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\)
f) \(=\left(\sqrt{x}+\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)\)
Chọn D.
Ta có: A = sin2(a + b) –sin2a - sin2b
= ( sina.cosb + cosa.sinb) 2 - sin2a - sin2b
= sin2a.cos2b + 2sina.cosb.cosa.sinb + cos2a.sin2b - sin 2a - sin2b
= sin2a( cos2b - 1) + sin2b( cos2a - 1) + 2.sina.cosa.sinb.cosb
= - sin2a.sin2b - sin2b.sin2a + 2.sina.cosa.sinb.cosb
= 2sina.sinb( cosa.cosb - sina.sinb) = 2.sina.sinb.cos( a + b).