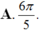
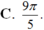
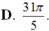
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tham khảo:
a)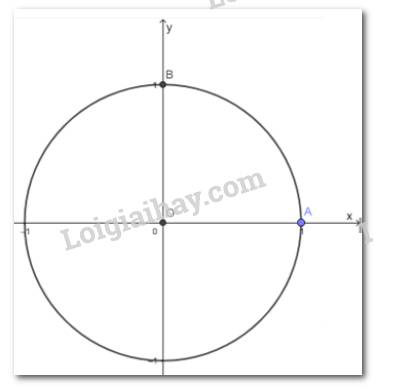 
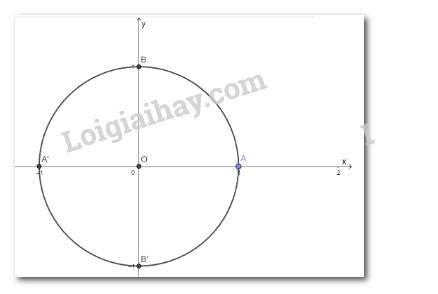
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)
Tham khảo:
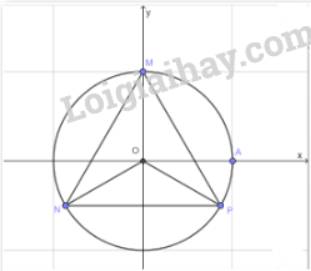
\(\begin{array}{l}(OM,ON) = (OA,ON) - (OA,OM) = \frac{{2\pi }}{3}\\ \Rightarrow \widehat {MON} = {120^0}\\\widehat {MOP} = \widehat {MOA} + \widehat {AOP} = {90^0} + {30^0} = {120^0}\\ \Rightarrow \widehat {NOP} = {360^0} - {120^0} - {120^0} = {120^0}\end{array}\)
Cung MP = cung NP = cung NM
\(\Rightarrow MP = NP = NM\)
\(\Rightarrow \Delta MNP\) đều
a, Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(135^o+n\cdot360^o,n\in Z\)
Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(-80^o+m\cdot360^o,m\in Z\)
Số đo của góc lượng giác (Oa, Ob) trong Hình 7 là \(415^o+k\cdot360^o,k\in Z\)
b, \(\left(Oa,Ob\right)+\left(Ob,Oc\right)=135^o+n\cdot360^o+\left(-80^o\right)+m\cdot360^o\\ =55^o+\left(n+m\right)\cdot360^o\\ =415^o+\left(n+m-1\right)\cdot360^o\\ =415^o+k\cdot360^o=\left(Oa,Oc\right)\)
Với \(k=n+m-1;n,m,k\in Z\)
a) Hoành độ của điểm M và M’ bằng nhau
Tung độ của điểm M và M’ đối nhau
b) Mối liên hệ giữa các giá trị lượng giác tương ứng của hai góc lượng giác \(\alpha \,\,v\`a \,\, - \alpha \)
Ta có: \(\left(OA,OM\right)=120^o+k\cdot360^o,k\in Z\\ \left(OA,ON\right)=-75^o+k\cdot360^o,k\in Z\)
Chọn D.
Ta có nhận xét như sau: