b. PTHĐGĐ của hai hàm số:

\(x+2=-2x+1\)

\(\Rightarrow x=-\dfrac{1}{3}\)

Thay x vào hs đầu tiên: \(y=-\dfrac{1}{3}+2=\dfrac{5}{3}\)

Tọa độ điểm \(A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\)

b: Tọa độ giao điểm là:

\(\left\{{}\begin{matrix}x+2=-2x+1\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)

\(b,\text{PT hoành độ giao điểm: }x+2=-2x+1\Leftrightarrow3x=-1\\ \Leftrightarrow x=-\dfrac{1}{3}\Leftrightarrow y=\dfrac{5}{3}\Leftrightarrow A\left(-\dfrac{1}{3};\dfrac{5}{3}\right)\\ c,\text{Gọi }y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \Leftrightarrow\left\{{}\begin{matrix}a=2;b\ne1\\-\dfrac{1}{3}a+b=\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=\dfrac{7}{3}\end{matrix}\right.\\ \Leftrightarrow y=2x+\dfrac{7}{3}\)

Bạn viết rõ đề bài ra nhé.

Lời giải:

a.

Đồ thị xanh lá: $y=2x+1$
Đồ thị xanh dương: $y=x-3$
b.

PT hoành độ giao điểm:
$y=2x+1=x-3$
$\Leftrightarrow x=-4$

$y=x-3=(-4)-3=-7$
Vậy tọa độ điểm $M$ là $(-4;-7)$

b, PT hoành độ giao điểm là \(2x-1=-x+5\Leftrightarrow3x=6\Leftrightarrow x=2\Leftrightarrow y=3\)

\(\Leftrightarrow A\left(2;3\right)\)

Vậy A(2;3) là tọa độ giao điểm 2 đths

\(b,\text{PT hoành độ giao điểm: }2x=-2x+4\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow A\left(1;2\right)\)

làm ơn ai làm nhanh hộ mình với hãy giúp mik 

(đơn vị đo trên các trục tọa độ là xentimet)

Lời giải:

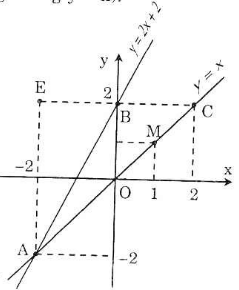
a) Vẽ đường thẳng qua O(0; 0) và điểm M(1; 1) được đồ thị hàm số y = x. Vẽ đường thẳng qua B(0; 2) và E(-1; 0) được đồ thị hàm số y = 2x + 2.

b) Tìm tọa độ của điểm A: giải phương trình 2x + 2 = x, tìm được x = -2. Từ đó tìm được x = -2, từ đó tính được y = -2, ta có A(-2; -2).

c) Qua B(0; 2) vẽ đường thẳng song song với Ox, đường thẳng này có phương trình y = 2 và cắt đường thẳng y = x tại C.

a) Đồ thị hàm số \(y=x\) là 1 đường thẳng đi qua 2 điểm O \(\left(0;0\right)\) và E\(\left(1;1\right)\)

Đồ thị hàm số \(y=2x+2\) là 1 đường thẳng đi qua 2 điểm B \(\left(0;2\right)\) và D \(\left(-1;0\right)\)

b) Hoành độ giao điểm A của 2 đường thẳng đã cho là nghiệm của pt:

\(x=2x+2\)

\(\Leftrightarrow\) \(x-2x=2\)

\(\Leftrightarrow\) \(-x=2\)

\(\Leftrightarrow\) \(x=-2\)

Tại \(x=-2\) thì giá trị của y là: \(y=2.\left(-2\right)+2=-2\)

Vậy tọa độ điểm A \(\left(-2;-2\right)\)

c) Đường thẳng song song với trục tung Ox và cắt trục hoành tại điểm B(0;2)

\(\Rightarrow\) Suy ra phương trình đường thẳng có dạng \(y=2x\)

Hoành độ giao điểm C của 2 đường thẳng y=2x và y=x là nghiệm của pt: 2x=x

\(\Rightarrow\) Tọa độ điểm C (2;2)

\(S_{ABC}=S_{ADO}+S_{BCOD}\)