Cho tam giác ABC, có BC = 6 cm, B ^ = 60 0 và C ^ = 40 0 . Hãy tính:
a, Chiều cao CH và cạnh AC
b, Diện tích tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(a,\sin\widehat{B}=\sin60^0=\dfrac{AC}{BC}=\dfrac{\sqrt{3}}{2}\Leftrightarrow AC=\dfrac{12\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\\ b,AC^2=CH\cdot BC\left(HTL.\Delta\right)\\ \Rightarrow CH=\dfrac{AC^2}{BC}=9\left(cm\right)\)
Tim Gia Tri Nho Nhat Cua
a) A = x - 4 can x + 9
b) B = x - 3 can x - 10
c ) C = x - can x + 1
d ) D = x + can x + 2

a, Diện tích tam giác ABC là
\(\dfrac{1}{2}.12.15=90cm^2\)
b, thiếu đề rồi bạn

Bài 2. 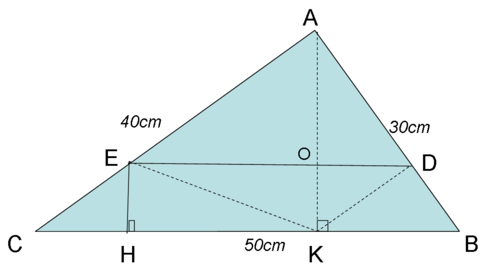
a) Trong tam giác vuông thì 2 cạnh góc vuông cũng chính là 2 đường cao của tam giác đó.
Vậy đường cao AB = 30 cm ; đường cao AC = 40 cm
Đường cao tam giác ABC còn lại đỉnh A là : 30 x 40 : 50 = 24 (cm)
b) S_ECK + S_DKB = CK x 6 : 2 + KB x 6 : 2 = (CK+KB) x 6 : 2 = 50 x 3 = 150 (cm2)
S_AEKD = 30 x 40 : 2 - 150 = 450 (cm2)
Xét tam giác AED và EDK chung đáy ED chiều cao AO = 24 - 6 = 18 (cm)
Tỉ lệ AO/OK = 18/6 = 3. Vậy S_AED = 3 x S_EDK
Diện tích tam giác AED là : 450 : (1+3) x 3 = 337,5 (cm2)
a, Áp dụng hệ thức giữa cạnh và góc trong tam giác vuông HCB chúng ta có
CH = 3 3 cm; A C sin C ≈ 5 , 28 c m
b, Tương tự, cũng áp dụng Pytago hoặc hệ thức giữa cạnh và góc trong tam giác vuông, tính được:
AH, BH => AB = 3,93cm. Ta có: S = 1 2 . 3 3 . 3 , 93 ≈ 10,21 c m 2