Cặp góc A1, B2 và cặp góc A4, B3 được gọi là hai cặp góc trong cùng phía
Tính:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()

a). đồng vị
b). so le trong
c). kề bù
d). đối đỉnh
e). trong cùng phía

a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)
\( \Rightarrow \widehat {{A_1}} + 40^\circ = 180^\circ \)
\( \Rightarrow \widehat {{A_1}} = 180^\circ - 40^\circ = 140^\circ \)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)
\(\widehat {{A_2}} = \widehat {{B_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong
\( \Rightarrow \) 2 góc đồng vị bằng nhau nên
\(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)
b) Ta có:
\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ + 40^\circ = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ + 140^\circ = 180^\circ \end{array}\)

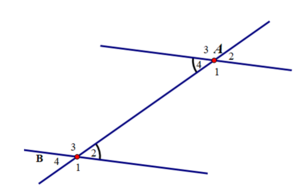
Ta có: ∠A1 + ∠A4 = 180o ⇒ ∠A1 = 180o - ∠A4 = 180o - 45o = 135o
∠B2 + ∠B3 = 180o ⇒ ∠B3 = 180o - ∠B2 = 180o- 45o = 135o

Hai cặp góc so le trong: ∠(A1 )và ∠(B3) ; ∠(A4) và ∠(B2 )
Bốn cặp góc đồng vị: ∠(A1 ) và ∠(B1 ) ; ∠(A2 ) và ∠(B2 ) ; ∠(A3) và ∠(B3 ) ; ∠(A4) và ∠(B4 )
Hai cặp góc so le ngoài: ∠(A3 ) và ∠(B1 ) ; ∠(A2 ) và ∠(B4 ) ;
Hai cặp góc trong cùng phía: ∠(A1 ) và ∠(B2 ) ; ∠(A4 ) và ∠(B3 ) ;
Hai cặp góc ngoài cùng phía: ∠(A2) và ∠(B1 ) ; ∠(A3 ) và ∠(B4 )