Chứng minh rằng, khi hai cuộn cảm thuần L1 và L2 mắc nối tiếp trong một mạch điện xoay chiều thì cuộn cảm tương đương có cảm kháng cho bởi: ZL = (L1 + L2)ω
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khi L1 và L2 mắc nối tiếp thì: U = U1 + U2 = - L1 – L2
U = -(L1 + L2) = với L = L1 + L2
Suy ra: ZL = Lω = L1ω + L2ω = +

Đáp án C
+ Khi L= L 1 và ω = 120 π rad/s thì U L có giá trị cực đại nên sử dụng hệ quả khi U L max ta có:
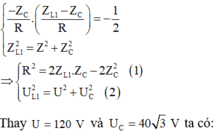
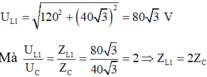
Chuẩn hóa: ![]() . Thay vào (1) ta có:
. Thay vào (1) ta có:
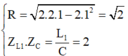
+ Khi L 2 = 2 L 1 thì vẫn thay đổi ω để U L max nên:
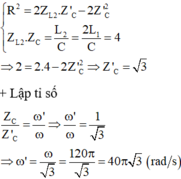

Khi L = L 1 thì dòng điện cùng pha với điện áp → hiện tượng cộng hưởng → Z C = Z L 1 = 2 π f L 1 .
Khi L = L 2 xảy ra cực đại điện áp hiệu dụng trên cuộn dây Z L 2 = R 2 + Z C 2 Z C ⇔ 2 π f L 2 = 50 2 + 2 π f L 1 2 2 π f L 1 → f = 25 Hz.
Đáp án A

Đáp án C
Khi 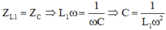
mạch có cộng hưởng ( L 1 = hằng số)
Khi 
![]()
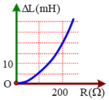
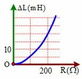
=> Dạng y = a x 2 → Một nhánh của Parabol
Khi
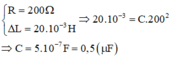

Chọn đáp án C
+ Khi ![]()
![]() mạch có cộng hưởng (L1= hằng số)
mạch có cộng hưởng (L1= hằng số)
+ Khi 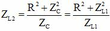
![]()
![]() Dạng
Dạng ![]() → Một nhánh của Parabol
→ Một nhánh của Parabol
+ Khi 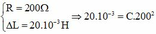
![]()
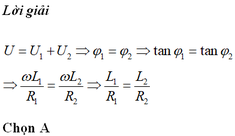
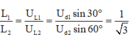
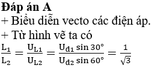
Gọi i = I0cosωt (A) là dòng điện qua mạch điện.
Vì L1 nối tiếp L2 nên u = u1 + u2; I1 = I2 = I.
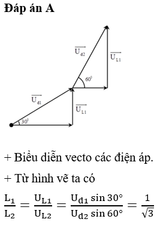
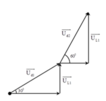
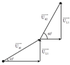
Các điện áp hai đầu L1 và L2 đều nhanh pha hơn i một góc π/2
→ U = U1 + U2 = I. ZL1 + I.ZL2 = I.(ZL1 + ZL2) = I.(L1.ω + L2.ω)
→ Tổng trở của mạch:
Vậy ZL = Z = (L1 + L2)ω