Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2x + 4y + 2z - 19 = 0 và mặt phẳng (P): x - 2y + 2z - 12 = 0. Tìm tọa độ tâm và bán kính của đường tròn đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
25 tháng 9 2018
Chọn C
Mặt cầu (S): x2 + y2 + z2 - 2x + 4y - 4z -16 = 0 có tâm I (1; -2; 2) bán kính R = 5
Khoảng cách từ I (1; -2; 2) đến mặt phẳng (P): x + 2y - 2z - 2 = 0 là 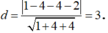
Mặt phẳng cắt mặt cầu theo giao tuyến là một đường tròn có bán kính là: ![]()

CM
15 tháng 5 2019
Mặt cầu (S) tâm I(1; -2; -1) bán kính R = 5
d(I,(P)) = 3 < R
Do đó (P) cắt (S) theo một đường tròn, gọi đường tròn đó là (C).

CM
31 tháng 3 2019
Chọn C.
Phương pháp: Lần lượt tìm các yếu tố tâm và bán kính của mặt cầu.
Cách giải: Tọa độ tâm mặt cầu thỏa mãn hệ




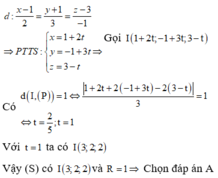
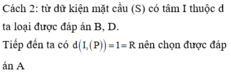



Gọi d là đường thẳng qua I và vuông góc với (P). Phương trình của d là
Tâm của (C) là điểm H = d ∩ (P). Để tìm H ta thay phương trình của d vào phương trình của (P).
Ta có: 1 + t - 2(-2 - 2t) + 2(-1 + 2t) - 12 = 0
Suy ra t = 1, do đó H = (2; -4; 1).
Bán kính của (C) bằng