Cho tam giác ABC cân tại A, các đường cao BD, CE cắt nhau tại H. Chứng minh AH là tia phân giác của B A C ^
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
CB chung
góc EBC=góc DCB
=>ΔEBC=ΔDCB
b: Xét ΔHBC có góc HCB=góc HBC
nên ΔHBC cân tại H
c: Xet ΔABH và ΔACH có
AB=AC
BH=CH
AH chung
=>ΔABH=ΔACH
=>góc BAH=góc CAH
=>AH làphân giác của góc BAC

a: Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
=>H là trực tâm
=>AH vuông góc BC
b: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC
c: Xét ΔAEH vuông tại E và ΔADH vuông tại D có
AH chung
góc EAH=góc DAH
=>ΔAEH=ΔADH
=>AE=AD và HE=HD
=>AH là trung trực của DE

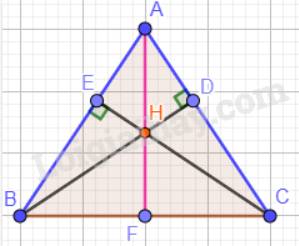
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).
Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ - 70^\circ - 70^\circ = 40^\circ \).
b) Xét tam giác vuông ADB và tam giác vuông AEC có:
AB = AC (tam giác ABC cân);
\(\widehat A\) chung.
Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).
c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.
Xét hai tam giác vuông AFB và AFC có:
AB = AC (tam giác ABC cân);
AF chung.
Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).
Vậy tia AH là tia phân giác của góc BAC.

Bạn tự vẽ hình ik nha
a. Xét tam giác ABD và tam giác ACE có:
góc D = góc E = 90* (gt)
AB = AC (gt)
góc A chung
=> tg ABD = tg ACE (c. huyền-g. nhọn)
b. Vì H là giao điểm của 2 dường cao BD và CE
Nên AH cũng là đường cao cùa tg ABC hay AH vuông góc BC
Do tg ABC là tam giác cân => AI là đường cao đồng thời cũng là dường trung tuyến => BI = CI => I là trung điểm của BC
c.Ta có: góc ACE = góc ABD (doc tg ABD = tg ACE)
và góc ABC = góc ACB
=> góc DBC = góc ECB
Ta có: BD vuông góc AC (gt)
CF vuông góc AC (gt)
=> CF song song BD (2 dường thẳng cùng vuông góc với 1 dường thẳng)
=> góc DBC = góc BCF ( so le trong)
Mà góc DBC = góc ECB
=> góc ECB = góc BCF
=> BC lá tia phân giác của góc ECF

a/ Xét \(\Delta ABD\left(D=1v\right)\) và \(\Delta ACE\left(E=1v\right)\) có:
góc A chung (gt)
AB = AC (\(\Delta ABC\) cân tại A)
=> \(\Delta ABD=\Delta ACE\) (ch-gn)
b/ Xét\(\Delta ABK\left(K=1v\right)\) và \(\Delta ACK\left(K=1v\right)\) có:
AB = AC (\(\Delta ABC\) cân tại A)
AK chung (gt)
=> \(\Delta ABK=\Delta ACK\) (ch-cgv)
=> góc BAK = góc CAK (hai góc tương ứng)
=> AK là tia phân giác của góc BAC
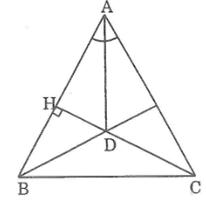
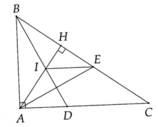

Chú ý H là trực tâm tam giác ABC, từ đó AH vừa là đường cao vừa là đường phân giác