D

D?

C

C

Có 4 hình tam giác.

Có 6 hình tứ giác

4hinh tam giac 5hinh tu giac 

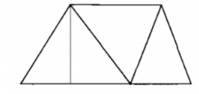
a) Có  3  hình tam giác.

b) Có  3  hình tứ giác.

3 hinh tu giac 3hinh tam giac ok

c

Đáp án: ý c

a: \(AB=\sqrt{\left(2+1\right)^2+\left(1-1\right)^2}=3\)

\(BC=\sqrt{\left(-1-2\right)^2+\left(-3-1\right)^2}=5\)

\(AC=\sqrt{\left(-1+1\right)^2+\left(-3-1\right)^2}=4\)

=>C=3+4+5=12

b: Tọa độ trọng tâm là:

\(\left\{{}\begin{matrix}x=\dfrac{-1+2-1}{3}=0\\y=\dfrac{1+1-3}{3}=-\dfrac{1}{3}\end{matrix}\right.\)

c: ABCD là hình bình hành

=>vecto AB=vecto DC

=>-1-x=2-(-1)=3 và -3-y=1-1=0

=>x=-4 và y=-3

a) Ta có :

\(\overrightarrow{AB}=3\\ \overrightarrow{BC}=5\\ \overrightarrow{AC}=4\)

Chu vi tam giác là : 

AB + BC + AC = 3 + 4 + 5 = 12

b) Toạ độ trọng tâm của tam giác ABC là :

\(\left(\dfrac{x_A+x_B+x_C}{3};\dfrac{y_A+y_B+y_C}{3}\right)=\left(\dfrac{-1+2+\left(-1\right)}{3};\dfrac{1+1+\left(-3\right)}{3}\right)=\left(0;-\dfrac{1}{3}\right)\)

c) Cho điểm D ( x ; y )

Để tứ giác ABCD là hình bình hành thì :

\(\overrightarrow{AD}=\overrightarrow{BC}\)

\(\Leftrightarrow\left(x+1;y-1\right)=\left(-3;-4\right)\\ \Leftrightarrow\left[{}\begin{matrix}x=-4\\y=-3\end{matrix}\right.\)

Vậy với D ( -4 ; -3 ) thì tứ giác ABCD là hình bình hành

là seo?

Gọi độ dài cạnh tam giác và cạnh tứ giác là a,b (cm) (a > b)

Cạnh của tam giác dài hơn cạnh của tứ giác là 10cm nên:

a – b = 10 cm => a = 10 + b

Chu vi tam giác bằng chu vi tứ giác nên:

a + a + a = 4 × b => 3 × a = 4 × b => 3 × (10 + b) = 4 × b => 30 + 3 × b = 4 × b => b = 30 cm

Suy ra a = 10 + 30 = 40 cm

Vậy độ dài cạnh tam giác là 40 cm và độ dài cạnh tứ giác là 30cm