Cho hình vuông ABCD cạnh a. Từ tâm O của hình vuông dựng đường thẳng Δ vuông góc với mặt phẳng (ABCD). Trên Δ lấy điểm S sao cho OS = a/2 . Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Qua O vẽ đường thẳng d vuông góc với (ABCD)
Khi đó d là trục đường tròn ngoại tiếp hình vuông ABCD
Gọi H là trung điểm của cạnh SA
Trong mặt phẳng (SAO) đường trung trực của đoạn SA cắt đường thẳng SO tại I , ta có: \(\Delta SAO\) đòng dạng \(\Delta SIH\)
\(\Rightarrow\dfrac{SA}{SO}=\dfrac{SI}{SH}\Leftrightarrow SI=\dfrac{SA.SH}{SO}=\dfrac{SA^2}{2SO}\)
Mà \(SA^2=SO^2+OA^2=\left(\dfrac{a}{2}\right)^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2=\dfrac{3a^2}{4}\)
\(\Leftrightarrow SA=\dfrac{a\sqrt{3}}{2}\)
Khi đó \(SI=\dfrac{3a^2}{\dfrac{4}{2.\dfrac{a}{2}}}=\dfrac{3a}{4}\)
Mặt khác \(\left\{{}\begin{matrix}IS=IA\\IA=IB=IC=ID\end{matrix}\right.\)
\(\Rightarrow IS=IA=IB=IC=ID=\dfrac{3a}{4}\)
Vậy mặt cầu ngoại tiếp hình chóp S.ABCD có tâm là I và bán kính \(R=SI=\dfrac{3a}{4}\)
Diện tích mặt cầu là: \(S=4\pi R^2=4\pi.\left(\dfrac{3a}{4}\right)^2=\dfrac{9\pi\pi^2}{4}\)
Thể tích khối cầu là: \(V=\dfrac{4}{3}\pi R^2=\dfrac{4}{3}\pi.\left(\dfrac{3a}{4}\right)^2=\dfrac{9\pi\pi^2}{16}\)

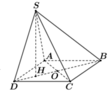
Xác định được ![]()
Tính được ![]()
![]()
Suy ra tam giác SBD vuông tại S. Vậy các đỉnh S, A, C cùng nhìn xuống BD dưới một góc vuông nên ![]()
Chọn B.

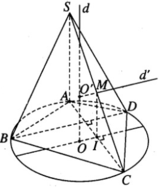
Trong mặt phẳng chứa đường tròn tâm O ngoại tiếp tứ giác ABCD ta kẻ đường kính qua O vuông góc với dây cung AC tại I. Ta có IA = IC và OI // BD. Gọi O’ là tâm mặt cầu đi qua 5 đỉnh của hình chóp. Khi đó điểm O’ phải nằm trên trục d của đường tròn ngoại tiếp tứ giác ABCD. Ta có d ⊥ (ABCD) tại O. Gọi M là trung điểm của cạnh SC. Ta có MI // SA nên MI ⊥ (ABCD) tại I. Từ M kẻ đường thẳng d’ // OI cắt d tại O’. Vì d′ ⊥ (SAC) tại M nên ta có O’C = O’S và O’C là bán kính r của mặt cầu ngoại tiếp hình chóp S.ABCD
Ta có:

Chọn đáp án A
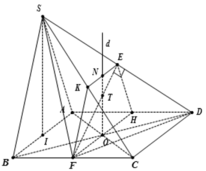
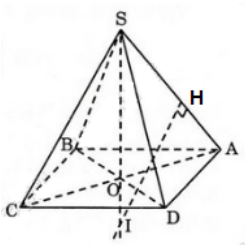
+ Gọi O là tâm của hình vuông ABCD. Qua O ta dựng đường thẳng d vuông góc với mặt đáy.
+ Gọi E, K, F, H, N lần lượt là trung điểm của các đoạn thẳng SD, SC, BC, AD, EK
+ Ta có tam giác SDF là tam giác cân tại F. Vì FD = FS = a 5 (độc giả tự chứng minh)
Suy ra FE ⊥ SD
Mặt khác, ta có KE // FH (Vì cùng song song với CD). Nên 4 điểm K, E, F, H đồng phẳng
+ Trong mặt phẳng (KEFH), gọi T là giao điểm của FE và ON.
Ta có T là tâm mặt cầu ngoại tiếp hình chóp S. ABCD
+ Ta có tam giác EKO là tam giác đều cạnh a. Nên
![]()
Bán kính mặt cầu là
![]()
+ Xét tam giác vuông TOB vuông tại B, ta có
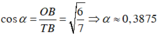

Đáp án D
Gọi H là trung điểm của AB, do tam giác SAB đều nên SH ⊥ AB mà (SAB) ⊥ (ABCD) nên SH ⊥ (ABCD)
Gọi O là tâm của hình vuông ABCD, d là đường thẳng qua O và song song SH thì d ⊥ (ABCD) hay d là trục đường tròn ngoại tiếp hình vuông ABCD
Trong mặt phẳng (SAB) từ G kẻ đường thẳng vuông góc với (SAB) cắt d tại I thì I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD, bán kính R = IS.
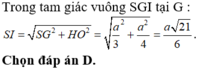

Đáp án D
Ta có mặt cầu S(A;r) tiếp xúc với mặt phẳng (SBC) khi và chỉ khi r = d(A; (SBC)).
Hạ AH ⊥ SB tại H. Do BC ⊥ AB và BC ⊥ SA nên BC ⊥ (SAB) , suy ra BC ⊥ AH.
Mặt khác AH ⊥ SB nên AH ⊥ (SBC) hay d(A; (SBC)) = AH Xét tam giác vuông SAB ta có:
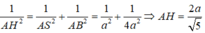





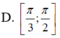
Mặt khác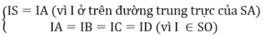
Suy ra Í=IIA=IB=IC=ID=3a/4
Vậy mặt cầu ngoại tiếp hình chóp S.ABCD có tâm I và bán kính R=SI=3a/4
Diện tích mắt cầu là:
Thể tích khối cầu là: