Gọi S là tập hợp tất cả các giá trị của tham số m ∈ ℤ và phương trình log m x - 5 x 2 - 6 x + 12 = log m x - 5 x + 2 có nghiệm duy nhất. Tìm số phân tử của S .
A. 2
B. 3
C. 0
D. 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ: \(mx-5>0\) ; \(x>-2\)
\(log_{mx-5}\left(x^2-6x+12\right)=log_{mx-5}\left(x+2\right)\)
\(\Rightarrow x^2-6x+12=x+2\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
TH1: \(x=2\) là nghiệm duy nhất \(\Rightarrow\left\{{}\begin{matrix}m.2-5>0\\m.5-5< 0\end{matrix}\right.\) \(\Rightarrow\) ktm
TH2: \(x=5\) là nghiệm duy nhất \(\Rightarrow\left\{{}\begin{matrix}m.2-5< 0\\m.5-5>0\end{matrix}\right.\)
\(\Rightarrow1< m< \dfrac{5}{2}\Rightarrow m=2\)

Lời giải:
$f(x)=m^2(x^4-1)+m(x^2-1)-6(x-1)=(x-1)[m^2(x+1)(x^2+1)+m(x+1)-6]$
Để $f(x)\geq 0$ với mọi $x\in\mathbb{R}$ thì:
$m^2(x+1)(x^2+1)+m(x+1)-6=Q(x)(x-1)^k$ với $k$ là số lẻ
$\Rightarrow h(x)=m^2(x+1)(x^2+1)+m(x+1)-6\vdots x-1$
$\Rightarrow h(1)=0$
$\Leftrightarrow 4m^2+2m-6=0$
$\Leftrightarrow 2m^2+m-3=0$
$\Leftrightarrow (m-1)(2m+3)=0\Rightarrow m=1$ hoặc $m=\frac{-3}{2}$
Thay các giá trị trên vào $f(x)$ ban đầu thì $m\in \left\{1; \frac{-3}{2}\right\}$
Tổng các giá trị của các phần tử thuộc $S$: $1+\frac{-3}{2}=\frac{-1}{2}$

Đáp án A.
Phương trình đã cho tương đương với
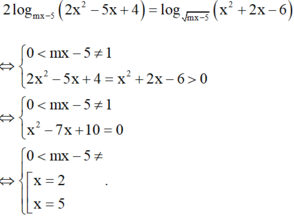
Để phương trình có nghiệm duy nhất
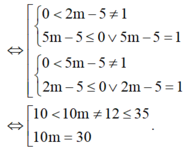
Do 10 m ∈ ℤ nên có 15 giá trị m thỏa mãn yêu cầu bài toán.

Đáp án A.
Phương trình đã cho tương đương với
2 log m x − 5 2 x 2 − 5 x + 4 = log m x − 5 x 2 + 2 x − 6
⇔ 0 < m x − 5 ≠ 1 2 x 2 − 5 x + 4 = x 2 + 2 x − 6 > 0 ⇔ 0 < m x − 5 ≠ 1 x 2 − 7 x + 10 = 0 ⇔ 0 < m x − 5 ≠ 1 x = 2 x = 5 .
Để phương trình có nghiệm duy nhất
⇔ 0 < 2 m − 5 ≠ 1 5 m − 5 ≤ 0 ∨ 5 m − 5 = 1 0 < 5 m − 5 ≠ 1 2 m − 5 ≤ 0 ∨ 2 m − 5 = 1 ⇔ 10 < 10 m ≠ 12 ≤ 35 10 m = 30 .
Do 10 m ∈ ℤ nên có 15 giá trị m thỏa mãn yêu cầu bài toán
Chọn A
Phương pháp:
- Tìm điều kiện xác định.
- Giải phương trình tìm nghiệm và tìm điều kiện để phương trình có nghiệm duy nhất.