Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (-1; 2; 4) và B (0; 1; 5). Gọi (P) là mặt phẳng đi qua A sao cho khoảng cách từ B đến (P) là lớn nhất. Khi đó, khoảng cách d từ O đến mặt phẳng (P) bằng bao nhiêu?
A . d = - 3 3
B . d = 3
C . d = 1 3
D . d = 1 3


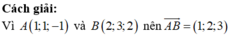

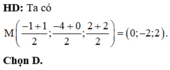

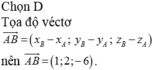



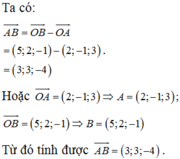
Chọn D
Gọi H là hình chiếu của B trên mặt phẳng (P) khi đó ta có BH là khoảng cách từ điểm B đến mặt phẳng (P). Ta luôn có BH ≤ AB do đó khoảng cách từ B đến mặt phẳng (P) lớn nhất khi H ≡ A, khi đó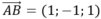 là véc tơ pháp tuyến của mặt phẳng (P)
là véc tơ pháp tuyến của mặt phẳng (P)
Vậy phương trình mặt phẳng (P) đi qua A (-1; 2; 4) và có véc tơ pháp tuyến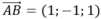 là x - y + z - 1 = 0
là x - y + z - 1 = 0
Vậy khoảng cách từ điểm O đến mặt phẳng (P) là: