Cho hình lăng trụ tam giác đều ABC. A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 600, cạnh AB=a. Tính thể tích V của khối lăng trụ ABC. A'B'C'.
A. V = 3 4 a 3
B. V = 3 4 a 3
C. V = 3 3 a 3 8
D. V = 3 a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
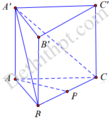
Kẻ A P ⊥ B C tan 60 ∘ = A ' A A P
⇒ A ' A = A P 3 = 3 . a 3 2 = 3 a 2 ⇒ V A B C C ' B ' = 2 V B ' . A B C = 2. 1 3 B B ' . S A B C = 2 3 . 3 a 2 . a 2 3 4 = a 3 3 4

Đáp án A
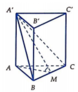
Gọi M là trung điểm BC. Ta có A ' M A ^ = 60 0
AM là trung tuyến trong tam giác đều cạnh a nên AM = a 3 2
![]()
![]()
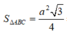
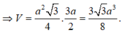

Chọn B
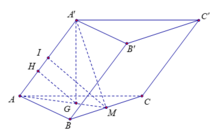
Ta có A ' G ⊥ A B C nên A ' G ⊥ B C ; B C ⊥ A M ⇒ B C ⊥ M A A '
Kẻ M I ⊥ A A ' ; B C ⊥ I M nên d A A ' ; B C = I M = a 3 4
Kẻ G H ⊥ A A ' , ta có
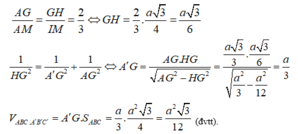

Chọn D
Diện tích đáy là B = S ∆ A B C = a 2 3 4 .
Chiều cao là h = d((ABC); (A'B'C')) = AA'
Do tam giác ABC là tam giác đều nên O là trọng tâm của tam giác ABC. Gọi I là trung điểm của BC, H là hình chiếu vuông góc của A lên A'I ta có:
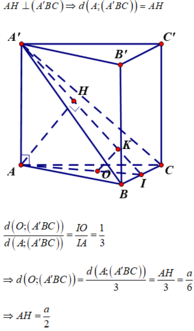
Xét tam giác A'AI vuông tại A ta có:
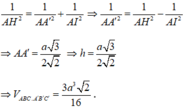

Đáp án A
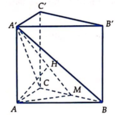
Gọi M là trung điểm của BC thì B C ⊥ A ' A M .
Từ A kẻ A H ⊥ A ' M , H ∈ A ' M . Khi đó A H ⊥ ( A ' B C ) .
Suy ra d A , A ' B C = A H = a 5 2 .
Góc giữa đường thẳng A ' B và mặt phẳng (ABC) bằng góc A ' M A ⏞ .
Theo giả thiết ta có A ' M A ⏞ = 60 °
Đặt AB = 2x thì A M = x 3 ; A ' A = 2 x 3 .
Suy ra A H = A ' A . A M A ' A 2 + A M 2 = 2 x 15 5
Từ giả thiết ta có 2 x 15 5 = a 5 2 ⇒ x = 5 a 15 12 Do đó
A A ' = 5 a 2 ; S A B C = 25 a 2 3 48
Vậy thể tích khối lăng trụ ABC.A'B'C' là V = 125 3 96 a 3 .

Chọn D
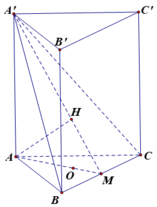
Gọi M là trung điểm của BC và H là hình chiếu của A trên A'M.
Ta có :
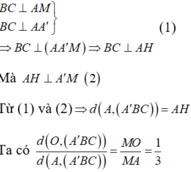
(do tính chất trọng tâm).

Xét tam giác vuông A'AM :
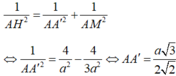
Suy ra thể tích lăng trụ ABC. A'B'C' là:


Chọn C
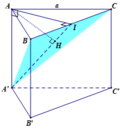
Gọi I là trung điểm của BC và H là hình chiếu vuông góc của A trên A'I. Khi đó ta có:
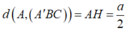
Trong tam giác vuông AA'I ta có:
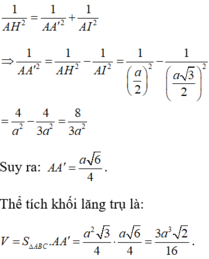

Đáp án D
Gọi I là trung điểm của cạnh BC, đặt AA’=x
Ta có
d ( O , ( A ' B C ) ) d ( A , ( A ' B C ) ) = O I A I = 1 3 ⇒ d ( A , ( A ' B C ) ) = a 2
Có V A ' A B C = 1 3 x . a 2 3 4 = 1 3 . a 2 . S A ' B C
Mà S A ' B C = 1 2 A ' I . B C = 1 2 x 2 + 3 a 2 4
⇒ x 3 = x 2 + 3 a 2 4 ⇔ 2 x 2 = 3 a 2 4 ⇒ x = a 3 2 2
⇒ V L T = a 3 2 2 . a 2 3 4 = 3 2 a 3 16
Chọn C
Gọi M là trung điểm của BC
=> AM ⊥ BC (1)
Ta có B C ⊥ A M B C ⊥ A A ' ⇒ B C ⊥ A ' M ( 2 )
Mặt khác A B C ∩ A ' B C = B C ( 3 )