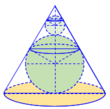
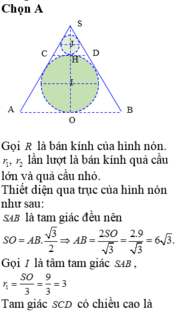
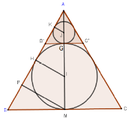
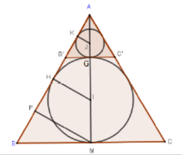
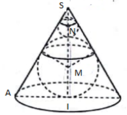
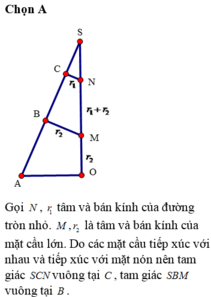
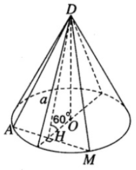
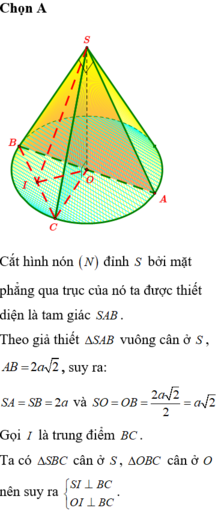
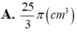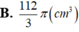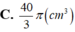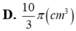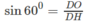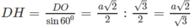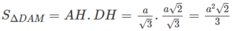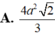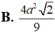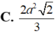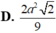Người ta chế tạo ra một món đồ chơi cho trẻ em theo các công đoạn như sau: Trước tiên, chế tạo tra một mặt nón tròn xoay có góc ở đỉnh là
2
β
=
60
°
bằng thủy tinh trong suốt. Sau đó đặt hai quả cầu nhỏ bằng thủy tinh có bán kính lớn, nhỏ khác nhau sao cho 2 mặt cầu tiếp xúc với nhau và đều tiếp xúc với mặt nón. Quả cầu lớn tiếp xúc với cả mặt đáy của mặt nón. Cho biết chiều cao của mặt nón bằng 9cm. Bỏ qua bề dày của những lớp vỏ thủy tinh, hãy tính tổng thể tích của hai khối cầu.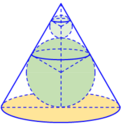
![]()
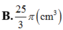
![]()
![]()