a: Thay x=1 và y=-1 vào (d), ta được:

\(\left(m-2\right)\cdot1+m+1=-1\)

=>m-2+m+1=-1

=>2m-1=-1

=>2m=0

=>m=0

b: Thay y=0 vào y=x+2, ta được:

x+2=0

=>x=-2

Thay x=-2 và y=0 vào y=(m-2)x+m+1, ta được:

-2(m-2)+m+1=0

=>-2m+4+m+1=0

=>5-m=0

=>m=5

- Với \(m=0\Rightarrow y=-x^2-2\) chỉ có cực đại (thỏa mãn)

- Với \(m\ne0\) hàm chỉ có cực đại khi:

\(\left\{{}\begin{matrix}m< 0\\m\left(2m-1\right)\ge0\end{matrix}\right.\) \(\Leftrightarrow m< 0\)

Vậy \(m\le0\)

Vì hs y = (m-1)x +m +3 đi qua điểm (1; -4) nên ta đc :

-4 = (m-1) + m+3

<=> -4 = 2m + 2

<=> m =-3

1) Đặt tên cho dễ giải nè:

(d1) : y= (m-1) x + m+ 3

(d2) : y = -2x + 1

(d1) // (d2) <=> m - 1 = -2 và m+ 3 \(\ne\)1

<=> m = -1 và m \(\ne\)-2 

Chọn D.

TXĐ: D = R.

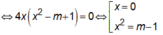
Đồ thị hàm số có 3 điểm cực trị ⇔ y' = 0 có ba nghiệm phân biệt  ⇔ m -1 > 0  ⇔ m > 1(*) 

3 điểm cực trị của đồ thị hàm số là: A(0;1), 

Hàm số đã cho là hàm số chẵn nên đồ thị hàm số nhận Oy làm trục đối xứng

Ta có 

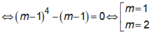
Kết hợp với điều kiện (*) => m = 2 

Làm theo bào toán trắc nghiệm như sau:

Hàm số đã cho có 3 điểm cực trị khi ab < 0  

Chỉ có đáp án D thỏa mãn.

a.

ĐTHS song với với đường thẳng đã cho khi:

\(\left\{{}\begin{matrix}m-2=-1\\m+3\ne3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=1\\m\ne0\end{matrix}\right.\) \(\Rightarrow m=1\)

b.

Gọi A là giao điểm của ĐTHS và \(y=2x+4\Rightarrow y_A=2\)

\(\Rightarrow2x_A+4=2\Rightarrow x_A=-1\)

\(\Rightarrow A\left(-1;2\right)\)

Thế tọa độ A vào (1):

\(-1\left(m-2\right)+m+3=2\Leftrightarrow5=2\left(ktm\right)\)

Vậy ko tồn tại m thỏa mãn yêu cầu đề bài